rvar: The Random Variable Datatype

Introduction

This vignette describes the rvar() datatype, a multidimensional, sample-based representation of random variables designed to act as much like base R arrays as possible (e.g., by supporting many math operators and functions). This format is also the basis of the draws_rvars() format.

The rvar() datatype is inspired by the rv package and Kerman and Gelman (2007), though with a slightly different backing format (multidimensional arrays). It is also designed to interoperate with vectorized distributions in the distributional package, to be able to be used inside data.frame()s and tibble()s, and to be used with distribution visualizations in the ggdist package.

The `rvars` datatype

The rvar() datatype is a wrapper around a multidimensional array where the first dimension is the number of draws in the random variable. The most direct way to create a random variable is to pass such an array to the rvar() function.

For example, to create a “scalar” rvar, one would pass a one-dimensional array or a vector whose length (here 4000) is the desired number of draws:

x <- rvar(rnorm(4000, mean = 1, sd = 1))
x

## rvar<4000>[1] mean ± sd:
## [1] 1 ± 1

The default display of an rvar shows the mean and standard deviation of each element of the array.

We can create random vectors by adding an additional dimension beyond just the draws dimension to the input array:

n <- 4   # length of output vector
x <- rvar(array(rnorm(4000*n, mean = 1, sd = 1), dim = c(4000, n)))
x

## rvar<4000>[4] mean ± sd:
## [1] 1.01 ± 0.99  1.02 ± 0.99  0.98 ± 1.00  0.99 ± 1.02

Or we can create a random matrix:

rows <- 4
cols <- 3
x <- rvar(array(rnorm(4000 * rows * cols, mean = 1, sd = 1), dim = c(4000, rows, cols)))
x

## rvar<4000>[4,3] mean ± sd:
##      [,1]         [,2]         [,3]        
## [1,] 1.00 ± 0.98  1.00 ± 1.00  0.97 ± 1.00 
## [2,] 1.00 ± 1.01  1.01 ± 1.02  0.99 ± 0.99 
## [3,] 1.02 ± 1.01  0.99 ± 1.00  1.00 ± 0.99 
## [4,] 1.01 ± 1.01  1.02 ± 1.00  1.00 ± 1.01

Or any array up to an arbitrary number of dimensions. The array backing an rvar can be accessed (and modified, with caution) via draws_of():

str(draws_of(x))

##  num [1:4000, 1:4, 1:3] -0.6879 0.0448 0.3519 1.261 -0.2197 ...
##  - attr(*, "dimnames")=List of 3
##   ..$ : chr [1:4000] "1" "2" "3" "4" ...
##   ..$ : NULL
##   ..$ : NULL

While the above examples assume all draws come from a single chain, rvars can also contain samples from multiple chains. For example, if your array of draws has iterations as the first dimension and chains as the second dimension, you can use with_chains = TRUE to create an rvar that includes chain information:

iterations <- 1000
chains <- 4
rows <- 4
cols <- 3
x_array <- array(
  rnorm(iterations * chains * rows * cols, mean = 1, sd = 1),
  dim = c(iterations, chains, rows, cols)
)
x <- rvar(x_array, with_chains = TRUE)
x

## rvar<1000,4>[4,3] mean ± sd:
##      [,1]         [,2]         [,3]        
## [1,] 0.97 ± 1.00  1.00 ± 0.99  1.02 ± 0.99 
## [2,] 1.02 ± 1.00  0.99 ± 1.01  1.01 ± 0.99 
## [3,] 1.00 ± 1.00  1.00 ± 1.00  1.01 ± 1.00 
## [4,] 1.03 ± 0.99  1.05 ± 1.00  0.98 ± 1.00

Manual construction and modification of rvars in this way is not always recommended unless you need it for performance reasons: several other higher-level interfaces to constructing and manipulating rvars are described below.

`rvar_factor` and `rvar_ordered` subtypes

You can also use rvars to represent discrete distributions, using the rvar_factor() and rvar_ordered() subtypes. If you attempt to create an rvar using character values or a factor, it will automatically be treated as an rvar_factor:

x <- rvar(sample(c("a","b","c"), 4000, prob = c(0.7, 0.2, 0.1), replace = TRUE))
x

## rvar_factor<4000>[1] mode <entropy>:
## [1] a <0.74> 
## 3 levels: a b c

Numeric arrays with a "levels" attribute can also be passed to rvar_factor(). This (along with conversion of character values) means output from rstanarm::posterior_predict() and brms::posterior_predict() on categorical models can be passed directly to rvar_factor().

The default display shows the mode (as returned by modal_category()) and normalized entropy (entropy()), which is Shannon entropy scaled by the maximum possible entropy for a distribution with the same number of levels: thus 0 means all probability is concentrated in one category, and 1 means the distribution is uniform.

You can construct an ordered factor using rvar_ordered() (or by passing an ordered() vector to rvar()):

x <- rvar_ordered(sample(c("a","b","c"), 4000, prob = c(0.7, 0.2, 0.1), replace = TRUE))
x

## rvar_ordered<4000>[1] mode <dissent>:
## [1] a <0.55> 
## 3 levels: a < b < c

For rvar_ordered(), the default display is mode and dissention (dissent()), which is 0 when all probability is concentrated in one category, and 1 when the distribution is bimodal at opposite ends of the scale.

rvar_factors attempt to mimic factor() and rvar_ordereds attempt to mimic ordered()s, by implementing factor-specific functions like levels(). Comparison operations are also implemented where valid. For example, in x as defined above, approximately 90% of draws should be less than "b" (which means the "a" and "b" levels):

x <= "b"

## rvar<4000>[1] mean ± sd:
## [1] 0.9 ± 0.29

rvars also supply an implementation of match() and %in%, which can be especially useful with rvar_factors:

x %in% c("a", "c")

## rvar<4000>[1] mean ± sd:
## [1] 0.8 ± 0.4

The `draws_rvars` datatype

The draws_rvars() datatype, like all draws datatypes in posterior, contains multiple variables in a joint sample from some distribution (e.g. a posterior or prior distribution).

You can construct draws_rvars() objects directly using the draws_rvars() function. The input rvars must have the same number of chains and iterations, but can otherwise have different shapes:

d <- draws_rvars(x = x, y = rvar(rnorm(iterations * chains), nchains = 4))
d

## # A draws_rvars: 4000 iterations, 1 chains, and 2 variables
## $x: rvar_ordered<4000>[1] mode <dissent>:
## [1] a <0.55> 
## 3 levels: a < b < c
## 
## $y: rvar<4000>[1] mean ± sd:
## [1] -0.012 ± 0.98

Existing objects can also be converted to the draws_rvars() format using as_draws_rvars(). Below is the example_draws("multi_normal") dataset converted into the draws_rvars() format. This dataset has 100 iterations from 4 chains from the posterior of a a 3-dimensional multivariate normal model. The mu variable is a mean vector of length 3 and the Sigma variable is a \(3 \times 3\) covariance matrix:

post <- as_draws_rvars(example_draws("multi_normal"))
post

## # A draws_rvars: 100 iterations, 4 chains, and 2 variables
## $mu: rvar<100,4>[3] mean ± sd:
## [1] 0.051 ± 0.11  0.111 ± 0.20  0.186 ± 0.31 
## 
## $Sigma: rvar<100,4>[3,3] mean ± sd:
##      [,1]          [,2]          [,3]         
## [1,]  1.28 ± 0.17   0.53 ± 0.20  -0.40 ± 0.28 
## [2,]  0.53 ± 0.20   3.67 ± 0.45  -2.10 ± 0.48 
## [3,] -0.40 ± 0.28  -2.10 ± 0.48   8.12 ± 0.95

The draws_rvars() datatype works much the same way that other draws formats do; see the main package vignette at vignette("posterior") for an introduction to draws objects. One difference is that draws_rvars counts variables differently, because it allows variables to be multidimensional. For example, the post object above contains two variables, mu and Sigma:

variables(post)

## [1] "mu"    "Sigma"

But converted to a draws_list(), it contains one variable for each combination of the dimensions of its variables:

variables(as_draws_list(post))

##  [1] "mu[1]"      "mu[2]"      "mu[3]"      "Sigma[1,1]" "Sigma[2,1]"
##  [6] "Sigma[3,1]" "Sigma[1,2]" "Sigma[2,2]" "Sigma[3,2]" "Sigma[1,3]"
## [11] "Sigma[2,3]" "Sigma[3,3]"

Math with `rvar`s

The rvar() datatype implements most math operations, including basic arithmetic, functions in the Math and Summary groups, like log() and exp() (see help("groupGeneric") for a list), and more. Binary operators can be performed between multiple rvars or between rvars and numerics. A simple example:

mu <- post$mu
Sigma <- post$Sigma

mu + 1

## rvar<100,4>[3] mean ± sd:
## [1] 1.1 ± 0.11  1.1 ± 0.20  1.2 ± 0.31

Matrix multiplication is also implemented (using a tensor product under the hood). In R < 4.3, the normal matrix multiplication operator (%*%) cannot be properly implemented for S3 datatypes, so rvar uses %**% instead. In R ≥ 4.3, which does support matrix multiplication for S3 datatypes, you can use %*% to matrix-multiply rvars.

A trivial example:

Sigma %**% diag(1:3)

## rvar<100,4>[3,3] mean ± sd:
##      [,1]          [,2]          [,3]         
## [1,]  1.28 ± 0.17   1.05 ± 0.40  -1.21 ± 0.85 
## [2,]  0.53 ± 0.20   7.33 ± 0.89  -6.30 ± 1.44 
## [3,] -0.40 ± 0.28  -4.20 ± 0.96  24.35 ± 2.84

The set of mathematical functions and operators supported by rvars includes:

Group	Functions and operators
Arithmetic operators	`+`, `-`, `*`, `/`, `^`, `%%`, `%/%`
Logical operators	`&`, `\|`, `!`
Comparison operators	`==`, `!=`, `<`, `<=`, `>=`, `>`
Value matching	`match()`, `%in%`
Matrix multiplication	`%*%`, `%%` (R ≥ 4.3 only)
Basic functions	`abs()`, `sign()` `sqrt()` `floor()`, `ceiling()`, `trunc()`, `round()`, `signif()`
Logarithms and exponentials	`exp()`, `expm1()` `log()`, `log10()`, `log2()`, `log1p()`
Trigonometric functions	`cos()`, `sin()`, `tan()` `cospi()`, `sinpi()`, `tanpi()` `acos()`, `asin()`, `atan()`
Hyperbolic functions	`cosh()`, `sinh()`, `tanh()` `acosh()`, `asinh()`, `atanh()`
Special functions	`lgamma()`, `gamma()`, `digamma()`, `trigamma()`
Cumulative functions	`cumsum()`, `cumprod()`, `cummax()`, `cummin()`
Array transposition	`t()`, `aperm()`
Matrix decomposition	`chol()`
Matrix diagonals	`diag()`

Expectations and summary functions

The E() function is an alias of mean(), producing means within each cell of an rvar. For example, given mu:

mu

## rvar<100,4>[3] mean ± sd:
## [1] 0.051 ± 0.11  0.111 ± 0.20  0.186 ± 0.31

We can get the expectation of each cell of mu:

E(mu)

## [1] 0.05139284 0.11132363 0.18581977

Expectations of logical expressions are probabilities, and can be computed either with E() / mean() or with Pr(). Pr() is provided as notational sugar, but also checks that the input is a logical variable before taking the mean:

Pr(mu > 0)

## [1] 0.6600 0.6900 0.7025

More generally, the rvar data type provides two types of summary functions:

Summary functions that mimic base-R vector summary functions, except applied to rvar vectors. These apply their summaries over elements of the input vectors within each draw, generally returning an rvar of length 1. These functions are prefixed with rvar_ as a reminder that they return rvars. Here is an example of rvar_mean():
```
rvar_mean(mu)
```
```
## rvar<100,4>[1] mean ± sd:
## [1] 0.12 ± 0.11
```
Summary functions that summarise within elements of input vectors and over draws. These summary functions generally return base arrays (numeric or logical) of the same shape as the input rvar, and are especially useful for diagnostic summaries. These summary functions are not prefixed with rvar_ as they do not return rvars. Here is an example of mean():
```
mean(mu)
```
```
## [1] 0.05139284 0.11132363 0.18581977
```
You should expect the same values from these functions (though in a different shape) when you use them with summarise_draws(), for example:
```
summarise_draws(mu, mean)
```
```
## # A tibble: 3 × 2
##   variable   mean
##   <chr>     <dbl>
## 1 mu[1]    0.0514
## 2 mu[2]    0.111 
## 3 mu[3]    0.186
```

Here is a table of both types of summary functions:

	1. Summarise within draws, over elements	2. Summarise over draws, within elements
Output format of `res = f(x)`	`rvar` of length 1	`array` of same shape as input `rvar`
Help page	`help("rvar-summaries-within-draws")`	`help("rvar-summaries-over-draws")`
Numeric summaries	`rvar_median()` `rvar_sum()`, `rvar_prod()` `rvar_min()`, `rvar_max()`	`median()` `sum()`, `prod()` `min()`, `max()`
Mean	`rvar_mean()` N/A	`mean()`, `E()` `Pr()`: enforces that input is `logical`
Spread	`rvar_sd()` `rvar_var()` `rvar_mad()`	`sd()` `var()`, `variance()` `mad()`
Range	`rvar_range()` Note: `length(res) == 2`	`range()` Note: `dim(res) == c(2, dim(x))`
Quantiles	`rvar_quantile()` Note: `length(res) == length(probs)`	`quantile()` Note: `dim(res) == c(length(probs), dim(x))`
Logical summaries	`rvar_all()`, `rvar_any()`	`all()`, `any()`
Special value predicates	`rvar_is_finite()` `rvar_is_infinite()` `rvar_is_nan()` `rvar_is_na()` Note: `dim(res) == dim(x)`. These functions act within draws but do not summarise over elements.	`is.finite()` `is.infinite()` `is.nan()` `is.na()` Note: `res[i] == TRUE` if `x[i]` has any draws matching predicate (except for `is.finite()`, where all draws in `x[i]` must match)
Diagnostics	N/A	`ess_basic()`, `ess_bulk()`, `ess_quantile()`, `ess_sd()`, `ess_tail()`, `mcse_mean()`, `mcse_quantile()`, `mcse_sd()` `rhat()`, `rhat_basic()`

Constants

Constant rvars can be constructed by converting numeric vectors or arrays into rvars using as_rvar(), which will return an rvar with one draw and the same dimensions as its input:

const <- as_rvar(1:3)
const

## rvar<1>[3] mean ± sd:
## [1] 1 ± NA  2 ± NA  3 ± NA

While normally rvars must have the same number of draws to be used in the same expression, rvars with one draw are treated like constants, and can be combined with other rvars:

mu + const

## rvar<100,4>[3] mean ± sd:
## [1] 1.1 ± 0.11  2.1 ± 0.20  3.2 ± 0.31

Using existing R functions and expressions with `rvar`s

While rvars attempt to emulate as much of the functionality of base R arrays as possible, there are situations in which an existing R function may not work directly with an rvar. There are several approaches to solving this problem.

For example, say you wish to generate samples from the following expression for \(\mu\), \(\sigma\), and \(x\):

\[ \begin{align} \left[\begin{matrix}\mu_1 \\ \vdots \\ \mu_4 \end{matrix}\right] &\sim \textrm{Normal}\left(\left[\begin{matrix}1 \\ \vdots \\ 4 \end{matrix}\right],1\right)\\ \sigma &\sim \textrm{Gamma}(1,1)\\ \left[\begin{matrix}x_1 \\ \vdots \\ x_4 \end{matrix}\right] &\sim \textrm{Normal}\left(\left[\begin{matrix}\mu_1 \\ \vdots \\ \mu_4 \end{matrix}\right], \sigma\right) \end{align} \]

There are three different approaches you might take to doing this: converting existing R functions with rfun(), executing expressions of random variables with rdo(), or evaluating random number generator functions using rvar_rng().

Converting functions with `rfun()`

The rfun() wrapper converts an existing R function into a new function that rvars can be passed to it as arguments, and which will return rvars. We can use rfun() to convert the base rnorm() and rgamma() random number generating functions into functions that accept and return rvars:

rvar_norm <- rfun(rnorm)
rvar_gamma <- rfun(rgamma)

Then we can translate the above example into code using those functions:

mu <- rvar_norm(4, mean = 1:4, sd = 1)
sigma <- rvar_gamma(1, shape = 1, rate = 1)
x <- rvar_norm(4, mu, sigma)
x

## rvar<4000>[4] mean ± sd:
## [1] 1 ± 1.7  2 ± 1.7  3 ± 1.7  4 ± 1.8

While rfun()-converted functions work well for prototyping, they will generally speaking be slower than functions designed specifically for rvars. Thus, you may find you need to adopt other strategies (like rvar_rng(), described below; or re-writing functions to support rvar directly using math operators and/or the draws_of() function).

Evaluating expressions with `rdo()`

An alternative to rfun() is to use rdo(), which can be passed nearly-arbitrary R expressions. The expression will be executed multiple times to construct an rvar. E.g., we can write an expression for mu like in the above example:

mu <- rdo(rnorm(4, mean = 1:4, sd = 1))
mu

## rvar<4000>[4] mean ± sd:
## [1] 0.98 ± 0.98  2.02 ± 1.02  2.99 ± 1.01  3.99 ± 1.01

We can also control the number of draws using the ndraws argument:

mu <- rdo(rnorm(4, mean = 1:4, sd = 1), ndraws = 1000)
mu

## rvar<1000>[4] mean ± sd:
## [1] 0.96 ± 1.05  1.99 ± 1.03  2.98 ± 0.98  4.01 ± 0.99

rdo() expressions can also contain other rvars, so long as all rvars in the expression have the same number of draws. Thus, we can re-write the example above that used rfun() as follows:

mu <- rdo(rnorm(4, mean = 1:4, sd = 1))
sigma <- rdo(rgamma(1, shape = 1, rate = 1))
x <- rdo(rnorm(4, mu, sigma))
x

## rvar<4000>[4] mean ± sd:
## [1] 0.97 ± 1.7  2.05 ± 1.7  3.05 ± 1.7  4.02 ± 1.7

Like rfun(), rdo() is not necessarily fast, so you may find it more useful for prototyping than production code.

Evaluating random number generators with `rvar_rng()`

rvar_rng() is an alternative to rfun()/rdo() designed specifically to work with random number generating functions that follow the typical API of such functions in base R. Such functions, like rnorm(), rgamma(), rbinom(), etc all following this interface:

They have a first argument, n, giving the number of draws to take from the distribution.
Their arguments for distribution parameters (mean, sd, shape, rate, etc.) are vectorized.
They return a single vector of length n, representing n draws from the distribution.

You can use any function with this interface with rvar_rng(), and it will adapt it to be able to take rvar arguments and return an rvar, as follows:

mu <- rvar_rng(rnorm, 4, mean = 1:4, sd = 1)
sigma <- rvar_rng(rgamma, 1, shape = 1, rate = 1)
x <- rvar_rng(rnorm, 4, mu, sigma)
x

## rvar<4000>[4] mean ± sd:
## [1] 1 ± 1.8  2 ± 1.8  3 ± 1.8  4 ± 1.8

In contrast to the rfun() and rdo() examples above, rvar_rng() takes advantage of the existing vectorization of the underlying random number generating function to execute quickly.

Broadcasting

Broadcasting for rvars does not follow R’s vector recycling rules. Instead, when two variables with different dimensions are being used with basic arithmetic functions, dimensions are added until both variables have the same number of dimensions. If two variables \(x\) and \(y\) differ on the length of dimension \(d\), they can be broadcast to the same size so long as one of the variables has dimension \(d\) of size 1. Then that variable will be broadcast up to the same size as the other variable along that dimension. If two variables disagree on the size of a dimension and neither has size 1, it is an error.

For example, consider this random matrix:

X <- rdo(rnorm(12, 1:12), dim = c(4,3))
X

## rvar<4000>[4,3] mean ± sd:
##      [,1]          [,2]          [,3]         
## [1,]  0.99 ± 1.00   5.00 ± 1.00   9.02 ± 0.99 
## [2,]  1.98 ± 1.02   5.99 ± 1.01   9.96 ± 1.00 
## [3,]  3.03 ± 0.98   6.99 ± 1.00  11.03 ± 0.99 
## [4,]  3.99 ± 1.01   7.99 ± 0.99  11.98 ± 1.02

And this vector of length 3:

y <- rdo(rnorm(3, 3:1))
y

## rvar<4000>[3] mean ± sd:
## [1] 3.00 ± 1.00  2.02 ± 0.99  0.96 ± 0.99

If we attempt to add X and y, it will produce an error as vectors are by default treated as column vectors, and y has length 3 while columns of X have length 4:

X + y

## Error: Cannot broadcast array of shape [4000,3,1] to array of shape [4000,4,3]:
## All dimensions must be 1 or equal.

By contrast, R arrays of the same shape will simply recycle y until it is the same length as X (regardless of the dimensions). Thus will produce a result, though likely not the intended result:

mean(X) + mean(y)

##          [,1]      [,2]      [,3]
## [1,] 3.990551  7.019104  9.979782
## [2,] 3.995785  6.951943 12.961398
## [3,] 3.997008  9.996424 13.053459
## [4,] 6.988434 10.011049 12.945383

On the other hand, if y were a row vector…

row_y = t(y)
row_y

## rvar<4000>[1,3] mean ± sd:
##      [,1]         [,2]         [,3]        
## [1,] 3.00 ± 1.00  2.02 ± 0.99  0.96 ± 0.99

…it would have the same number of columns as X and contain only one row, so it can be broadcast along rows of X:

X + row_y

## rvar<4000>[4,3] mean ± sd:
##      [,1]      [,2]      [,3]     
## [1,]  4 ± 1.4   7 ± 1.4  10 ± 1.4 
## [2,]  5 ± 1.4   8 ± 1.4  11 ± 1.4 
## [3,]  6 ± 1.4   9 ± 1.4  12 ± 1.4 
## [4,]  7 ± 1.4  10 ± 1.4  13 ± 1.4

Slicing and conditionals

The [[ and [ operators implement all of the base array slicing operations, including numeric, character, and logical indices, as well as slicing arrays using a matrix of indices with [. The main difference between rvar slicing and base array slicing is that rvars default to drop = FALSE; i.e. they retain all dimensions of the original rvar array. For a complete list of rvar slicing types, see help("rvar-slice").

In addition to the base slicing operations, rvar also implements three slicing/conditioning methods that allow you to use other rvars to define a slice.

To demonstrate these operations, consider an rvar vector of two components:

component = rvar_rng(rnorm, 2, mean = c(1, 5))
component

## rvar<4000>[2] mean ± sd:
## [1] 1 ± 0.98  5 ± 0.99

Perhaps we want to create a mixture of these two components, mixture, with a mixing proportion of 0.75. We could create an index, i, that is a random variable indicating which component (1 or 2) determines the value of mixture on each draw:

i = rvar_rng(rbinom, 1, size = 1, p = 0.75) + 1L
i

## rvar<4000>[1] mean ± sd:
## [1] 1.7 ± 0.44

We can use several different approaches to create the mixture distribution

Subsetting `rvar`s by draw: `x[<logical rvar>]`

A slice x[i] where i is a scalar logical rvar returns a new rvar with the same shape as x, but containing only those draws where i is TRUE. Thus, we can use i == 2 to select draws from the second component and overwrite them in the first component, creating the mixture distribution:

mixture = component[[1]]
mixture[i == 2] = component[[2]][i == 2]
mixture

## rvar<4000>[1] mean ± sd:
## [1] 4 ± 2

The resulting mixture looks like this:

library(ggplot2)

## Warning: package 'ggplot2' was built under R version 4.2.3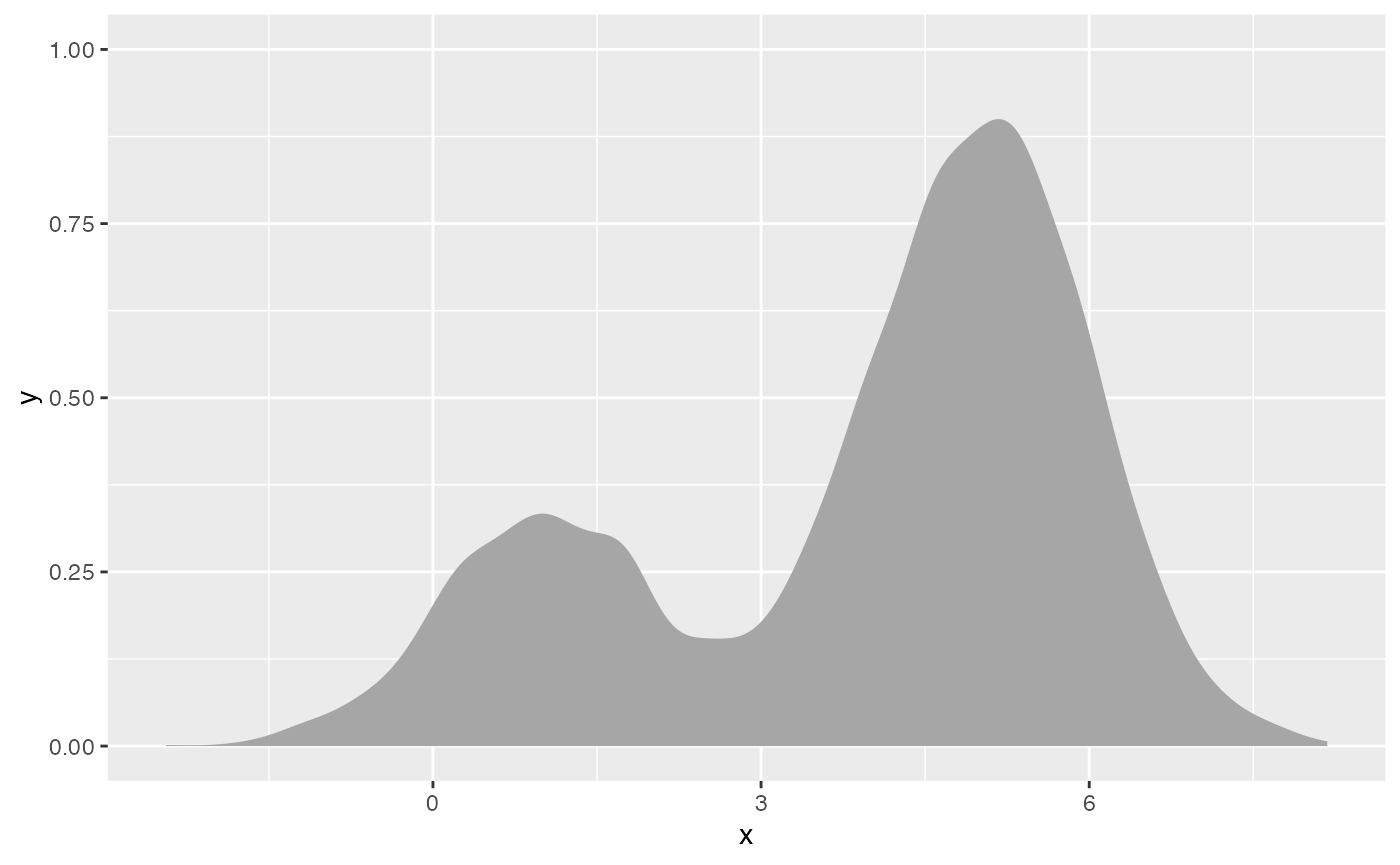

ggplot() + ggdist::stat_slab(aes(xdist = mixture))

See vignette("slabinterval", package = "ggdist") for more examples of visualizing distribution-type objects, including rvars.

Conditionals using `rvar_ifelse()`

You could create the same mixture using rvar_ifelse(test, yes, no), which broadcasts test, yes, and no to the same shape, then returns a new rvar containing draws from yes where test == TRUE and draws from no where test == FALSE.

Thus, we can create the mixture as follows:

x = rvar_ifelse(i == 1, component[[1]], component[[2]])
x

## rvar<4000>[1] mean ± sd:
## [1] 4 ± 2

Selecting different elements in each draw: `x[[<numeric rvar>]]`

The slice x[[i]], where i is a scalar numeric rvar, generalizes indexing when i is a scalar numeric. Within each draw of x, it selects the element of x corresponding to the value of i within that same draw.

Thus, since i in our example is a scalar numeric rvar whose values are either 1 or 2 within each draw, you can use it as an index directly on component to create the mixture:

x = component[[i]]
x

## rvar<4000>[1] mean ± sd:
## [1] 4 ± 2

This approach is also nice because it generalizes easily to more than two components.

Applying functions over `rvar`s

The rvar data type supplies an implementation of as.list(), which should give compatibility with the base R family of functions for applying functions over arrays: apply(), lapply(), vapply(), sapply(), etc. You can also manually use as.list() to convert an rvar into a list along its first dimension, which may be necessary for compatibility with some functions (like purrr:map()).

For example, given this multidimensional rvar…

set.seed(3456)
x <- rvar_rng(rnorm, 24, mean = 1:24)
dim(x) <- c(2,3,4)
x

## rvar<4000>[2,3,4] mean ± sd:
## , , 1
## 
##      [,1]       [,2]       [,3]      
## [1,]  1 ± 1.00   3 ± 0.98   5 ± 1.00 
## [2,]  2 ± 1.00   4 ± 1.00   6 ± 1.01 
## 
## , , 2
## 
##      [,1]       [,2]       [,3]      
## [1,]  7 ± 1.00   9 ± 1.00  11 ± 1.03 
## [2,]  8 ± 0.98  10 ± 0.99  12 ± 1.00 
## 
## , , 3
## 
##      [,1]       [,2]       [,3]      
## [1,] 13 ± 1.00  15 ± 1.00  17 ± 0.99 
## [2,] 14 ± 1.01  16 ± 1.00  18 ± 1.00 
## 
## , , 4
## 
##      [,1]       [,2]       [,3]      
## [1,] 19 ± 0.99  21 ± 0.99  23 ± 0.99 
## [2,] 20 ± 1.00  22 ± 1.00  24 ± 1.00

… you can apply functions along the margins using apply() (here, a silly example):

apply(x, c(1,2), length)

##      [,1] [,2] [,3]
## [1,]    4    4    4
## [2,]    4    4    4

One exception is that while apply() will work with an rvar input if your function returns base data types (like numerics), it will not give you simplified rvar arrays if your function returns an rvar. Thus, we supply the rvar_apply() function, which takes in either base arrays or rvar arrays and returns rvar arrays, and which also uses the rvar broadcasting rules to combine the results of the applied function.

For example, you can use rvar_apply() with rvar_mean() to compute the distributions of means along one margin of an array:

rvar_apply(x, 1, rvar_mean)

## rvar<4000>[2] mean ± sd:
## [1] 12 ± 0.29  13 ± 0.29

Or along multiple dimensions:

rvar_apply(x, c(2,3), rvar_mean)

## rvar<4000>[3,4] mean ± sd:
##      [,1]         [,2]         [,3]         [,4]        
## [1,]  1.5 ± 0.70   7.5 ± 0.69  13.5 ± 0.71  19.5 ± 0.70 
## [2,]  3.5 ± 0.70   9.5 ± 0.71  15.5 ± 0.72  21.5 ± 0.70 
## [3,]  5.5 ± 0.71  11.5 ± 0.72  17.5 ± 0.71  23.5 ± 0.70

Looping over `draws` and `rvar`s

The rvar datatype is also used in for_each_draw(), which allows you to loop over draws in a draws object or an rvar. for_each_draw(x, expr) converts x into a draws_rvars() object, then loops over each draw of x, executing the provided expression, expr. The expression can use the variables in x as if they were regular R arrays.

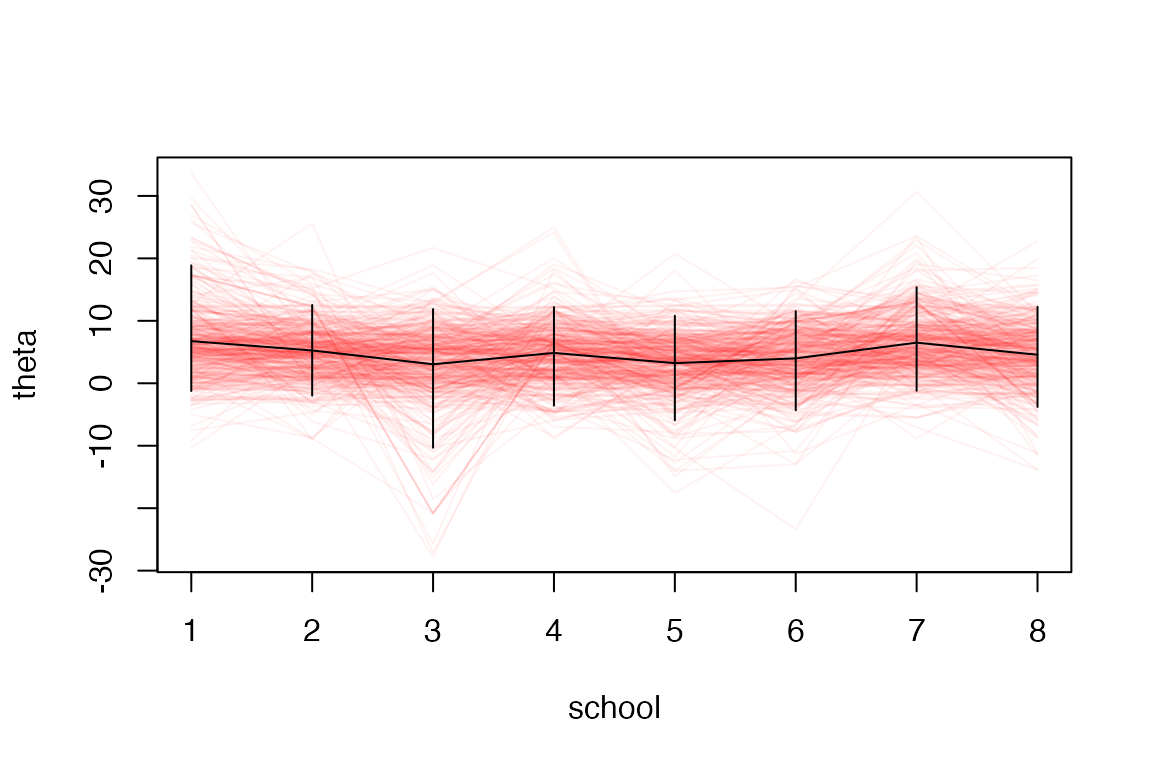
One application of for_each_draw() is in constructing base-R plots of individual draws (for ggplot2-based plotting of rvars, see the next section and the ggdist package). For example, it can be used to construct a parallel coordinates plot:

eight_schools <- as_draws_rvars(example_draws())

plot(1, type = "n",
  xlim = c(1, length(eight_schools$theta)),
  ylim = range(range(eight_schools$theta)),
  xlab = "school", ylab = "theta"
)

# use for_each_draw() to make a parallel coordinates plot of all draws
# of eight_schools$theta
for_each_draw(eight_schools, {
  lines(seq_along(theta), theta, col = rgb(1, 0, 0, 0.05))
})

# add means and 90% intervals
lines(seq_along(eight_schools$theta), mean(eight_schools$theta))
with(summarise_draws(eight_schools$theta), 
  segments(seq_along(eight_schools$theta), y0 = q5, y1 = q95)
)

As for_each_draw() will be slower than most other ways of manipulating draws, this function should generally not be used unless needed.

Using `rvar`s in data frames and in ggplot2

rvars can be used as columns in data.frame() or tibble() objects:

df <- data.frame(group = c("a","b","c","d"), mu)
df

##   group       mu
## 1     a 1 ± 1.02
## 2     b 2 ± 1.02
## 3     c 3 ± 0.99
## 4     d 4 ± 1.01

This makes them convenient for adding predictions to a data frame alongside the data used to generate the predictions. rvars can then be visualized with ggplot2 by passing them to the xdist and ydist aesthetics of the stat_... family of geometries in the ggdist package, such as stat_halfeye(), stat_lineribbon(), and stat_dotsinterval(). For example:

library(ggplot2)
library(ggdist)

## Warning: package 'ggdist' was built under R version 4.2.3

ggplot(df) +
  stat_halfeye(aes(y = group, xdist = mu))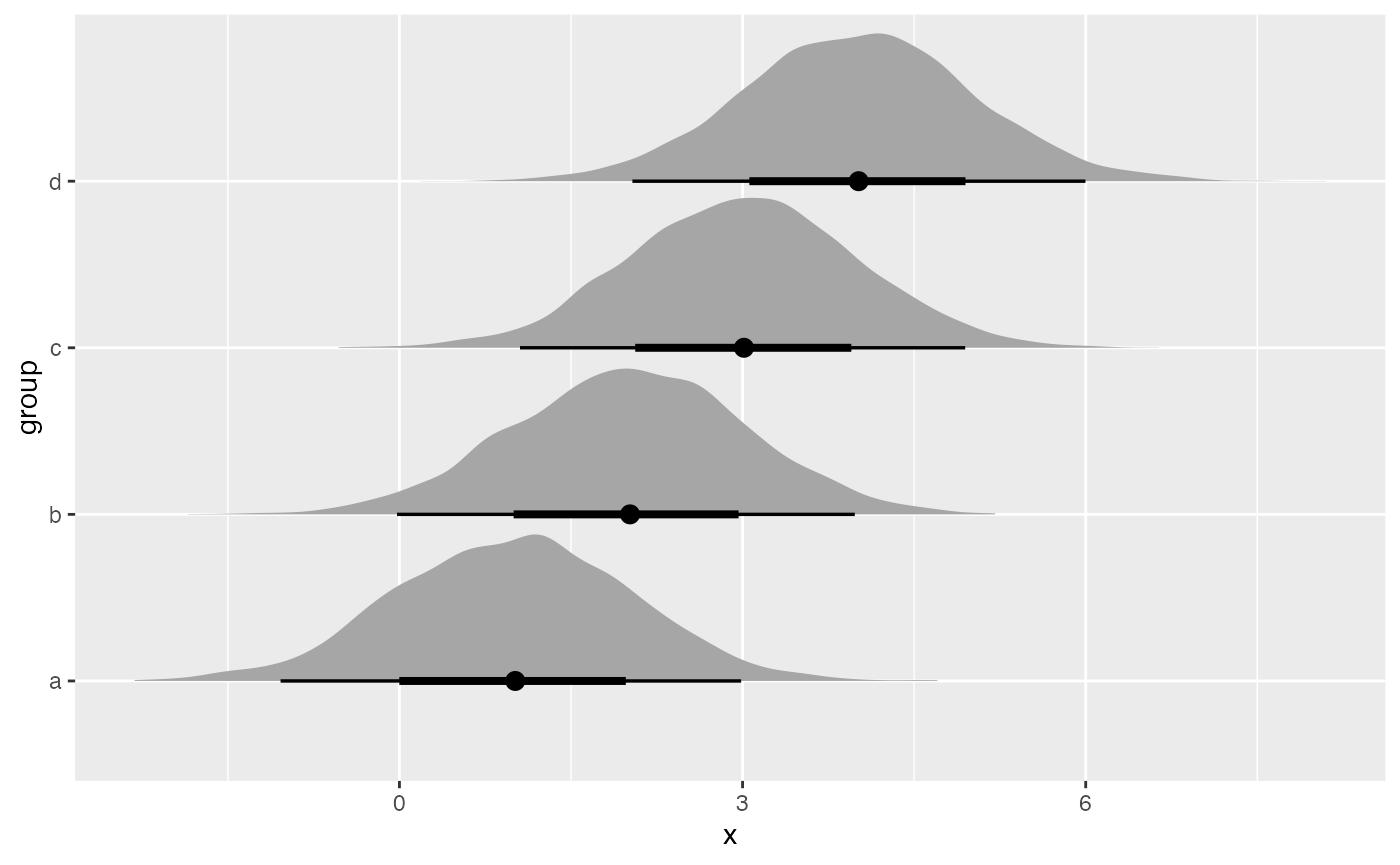

See vignette("slabinterval", package = "ggdist") or vignette("tidy-posterior", package = "tidybayes") for more examples.

Matthew Kay

2024-07-05

Introduction

The `rvars` datatype

`rvar_factor` and `rvar_ordered` subtypes

The `draws_rvars` datatype

Math with `rvar`s

Expectations and summary functions

Constants

Using existing R functions and expressions with `rvar`s

Converting functions with `rfun()`

Evaluating expressions with `rdo()`

Evaluating random number generators with `rvar_rng()`

Broadcasting

Slicing and conditionals

Subsetting `rvar`s by draw: `x[<logical rvar>]`

Conditionals using `rvar_ifelse()`

Selecting different elements in each draw: `x[[<numeric rvar>]]`

Applying functions over `rvar`s

Looping over `draws` and `rvar`s

Using `rvar`s in data frames and in ggplot2

rvar: The Random Variable Datatype

Matthew Kay

2024-07-05

Introduction

The rvars datatype

rvar_factor and rvar_ordered subtypes

The draws_rvars datatype

Math with rvars

Expectations and summary functions

Constants

Using existing R functions and expressions with rvars

Converting functions with rfun()

Evaluating expressions with rdo()

Evaluating random number generators with rvar_rng()

Broadcasting

Slicing and conditionals

Subsetting rvars by draw: x[<logical rvar>]

Conditionals using rvar_ifelse()

Selecting different elements in each draw: x[[<numeric rvar>]]

Applying functions over rvars

Looping over draws and rvars

Using rvars in data frames and in ggplot2

The `rvars` datatype

`rvar_factor` and `rvar_ordered` subtypes

The `draws_rvars` datatype

Math with `rvar`s

Using existing R functions and expressions with `rvar`s

Converting functions with `rfun()`

Evaluating expressions with `rdo()`

Evaluating random number generators with `rvar_rng()`

Subsetting `rvar`s by draw: `x[<logical rvar>]`

Conditionals using `rvar_ifelse()`

Selecting different elements in each draw: `x[[<numeric rvar>]]`

Applying functions over `rvar`s

Looping over `draws` and `rvar`s

Using `rvar`s in data frames and in ggplot2