The $variational() method of a CmdStanModel object runs
Stan's Automatic Differentiation Variational Inference (ADVI) algorithms.
The approximation is a Gaussian in the unconstrained variable space. Stan
implements two ADVI algorithms: the algorithm="meanfield" option uses a
fully factorized Gaussian for the approximation; the algorithm="fullrank"
option uses a Gaussian with a full-rank covariance matrix for the
approximation. See the
CmdStan User’s Guide
for more details.
Any argument left as NULL will default to the default value used by the
installed version of CmdStan.
variational(
data = NULL,
seed = NULL,
refresh = NULL,
init = NULL,
save_latent_dynamics = FALSE,
output_dir = getOption("cmdstanr_output_dir"),
output_basename = NULL,
sig_figs = NULL,
threads = NULL,
opencl_ids = NULL,
algorithm = NULL,
iter = NULL,
grad_samples = NULL,
elbo_samples = NULL,
eta = NULL,
adapt_engaged = NULL,
adapt_iter = NULL,
tol_rel_obj = NULL,
eval_elbo = NULL,
output_samples = NULL,
draws = NULL,
show_messages = TRUE,
show_exceptions = TRUE,
save_cmdstan_config = NULL
)Arguments
- data
(multiple options) The data to use for the variables specified in the data block of the Stan program. One of the following:
A named list of R objects with the names corresponding to variables declared in the data block of the Stan program. Internally this list is then written to JSON for CmdStan using
write_stan_json(). Seewrite_stan_json()for details on the conversions performed on R objects before they are passed to Stan.A path to a data file compatible with CmdStan (JSON or R dump). See the appendices in the CmdStan guide for details on using these formats.
NULLor an empty list if the Stan program has no data block.
- seed
(positive integer(s)) A seed for the (P)RNG to pass to CmdStan. In the case of multi-chain sampling the single
seedwill automatically be augmented by the the run (chain) ID so that each chain uses a different seed. The exception is the transformed data block, which defaults to using same seed for all chains so that the same data is generated for all chains if RNG functions are used. The only timeseedshould be specified as a vector (one element per chain) is if RNG functions are used in transformed data and the goal is to generate different data for each chain.- refresh
(non-negative integer) The number of iterations between printed screen updates. If
refresh = 0, only error messages will be printed.- init
(multiple options) The initialization method to use for the variables declared in the parameters block of the Stan program. One of the following:
A real number
x>0. This initializes all parameters randomly between[-x,x]on the unconstrained parameter space.;The number
0. This initializes all parameters to0;A character vector of paths (one per chain) to JSON or Rdump files containing initial values for all or some parameters. See
write_stan_json()to write R objects to JSON files compatible with CmdStan.A list of lists containing initial values for all or some parameters. For MCMC the list should contain a sublist for each chain. For other model fitting methods there should be just one sublist. The sublists should have named elements corresponding to the parameters for which you are specifying initial values. See Examples.
A function that returns a single list with names corresponding to the parameters for which you are specifying initial values. The function can take no arguments or a single argument
chain_id. For MCMC, if the function has argumentchain_idit will be supplied with the chain id (from 1 to number of chains) when called to generate the initial values. See Examples.A
CmdStanMCMC,CmdStanMLE,CmdStanVB,CmdStanPathfinder, orCmdStanLaplacefit object. If the fit object's parameters are only a subset of the model parameters then the other parameters will be drawn by Stan's default initialization. The fit object must have at least some parameters that are the same name and dimensions as the current Stan model. For thesampleandpathfindermethod, if the fit object has fewer draws than the requested number of chains/paths then the inits will be drawn using sampling with replacement. Otherwise sampling without replacement will be used. When aCmdStanPathfinderfit object is used as the init, if .psis_resamplewas set toFALSEandcalculate_lpwas set toTRUE(default), then resampling without replacement with Pareto smoothed weights will be used. Ifpsis_resamplewas set toTRUEorcalculate_lpwas set toFALSEthen sampling without replacement with uniform weights will be used to select the draws. PSIS resampling is used to select the draws forCmdStanVB, andCmdStanLaplacefit objects.A type inheriting from
posterior::draws. If the draws object has less samples than the number of requested chains/paths then the inits will be drawn using sampling with replacement. Otherwise sampling without replacement will be used. If the draws object's parameters are only a subset of the model parameters then the other parameters will be drawn by Stan's default initialization. The fit object must have at least some parameters that are the same name and dimensions as the current Stan model.
- save_latent_dynamics
(logical) Should auxiliary diagnostic information about the latent dynamics be written to temporary diagnostic CSV files? This argument replaces CmdStan's
diagnostic_fileargument and the content written to CSV is controlled by the user's CmdStan installation and not CmdStanR (for some algorithms no content may be written). The default isFALSE, which is appropriate for almost every use case. To save the temporary files created whensave_latent_dynamics=TRUEsee the$save_latent_dynamics_files()method.- output_dir
(string) A path to a directory where CmdStan should write its output CSV files. For MCMC there will be one file per chain; for other methods there will be a single file. For interactive use this can typically be left at
NULL(temporary directory) since CmdStanR makes the CmdStan output (posterior draws and diagnostics) available in R via methods of the fitted model objects. This can be set for an entire R session usingoptions(cmdstanr_output_dir). The behavior ofoutput_diris as follows:If
NULL(the default), then the CSV files are written to a temporary directory and only saved permanently if the user calls one of the$save_*methods of the fitted model object (e.g.,$save_output_files()). These temporary files are removed when the fitted model object is garbage collected (manually or automatically).If a path, then the files are created in
output_dirwith names corresponding to the defaults used by$save_output_files().
- output_basename
(string) A string to use as a prefix for the names of the output CSV files of CmdStan. If
NULL(the default), the basename of the output CSV files will be comprised from the model name, timestamp, and 5 random characters.- sig_figs
(positive integer) The number of significant figures used when storing the output values. By default, CmdStan represent the output values with 6 significant figures. The upper limit for
sig_figsis 18. Increasing this value will result in larger output CSV files and thus an increased usage of disk space.- threads
(positive integer) If the model was compiled with threading support, the number of threads to use in parallelized sections (e.g., when using the Stan functions
reduce_sum()ormap_rect()).- opencl_ids
(integer vector of length 2) The platform and device IDs of the OpenCL device to use for fitting. The model must be compiled with
cpp_options = list(stan_opencl = TRUE)for this argument to have an effect.- algorithm
(string) The algorithm. Either
"meanfield"or"fullrank".- iter
(positive integer) The maximum number of iterations.
- grad_samples
(positive integer) The number of samples for Monte Carlo estimate of gradients.
- elbo_samples
(positive integer) The number of samples for Monte Carlo estimate of ELBO (objective function).
- eta
(positive real) The step size weighting parameter for adaptive step size sequence.
- adapt_engaged
(logical) Do warmup adaptation?
- adapt_iter
(positive integer) The maximum number of adaptation iterations.
- tol_rel_obj
(positive real) Convergence tolerance on the relative norm of the objective.
- eval_elbo
(positive integer) Evaluate ELBO every Nth iteration.
- output_samples
(positive integer) Use
drawsargument instead.output_sampleswill be deprecated in the future.- draws
(positive integer) Number of approximate posterior samples to draw and save.
- show_messages
(logical) When
TRUE(the default), prints all output during the execution process, such as iteration numbers and elapsed times. If the output is silenced then the$output()method of the resulting fit object can be used to display the silenced messages.- show_exceptions
(logical) When
TRUE(the default), prints all informational messages, for example rejection of the current proposal. Disable if you wish to silence these messages, but this is not usually recommended unless you are very confident that the model is correct up to numerical error. If the messages are silenced then the$output()method of the resulting fit object can be used to display the silenced messages.- save_cmdstan_config
(logical) When
TRUE(the default), call CmdStan with argument"output save_config=1"to save a json file which contains the argument tree and extra information (equivalent to the output CSV file header). This option is only available in CmdStan 2.34.0 and later.
Value
A CmdStanVB object.
See also
The CmdStanR website (mc-stan.org/cmdstanr) for online documentation and tutorials.
The Stan and CmdStan documentation:
Stan documentation: mc-stan.org/users/documentation
CmdStan User’s Guide: mc-stan.org/docs/cmdstan-guide
Other CmdStanModel methods:
model-method-check_syntax,
model-method-compile,
model-method-diagnose,
model-method-expose_functions,
model-method-format,
model-method-generate-quantities,
model-method-laplace,
model-method-optimize,
model-method-pathfinder,
model-method-sample,
model-method-sample_mpi,
model-method-variables
Examples
# \dontrun{
library(cmdstanr)
library(posterior)
library(bayesplot)
color_scheme_set("brightblue")
# Set path to CmdStan
# (Note: if you installed CmdStan via install_cmdstan() with default settings
# then setting the path is unnecessary but the default below should still work.
# Otherwise use the `path` argument to specify the location of your
# CmdStan installation.)
set_cmdstan_path(path = NULL)
#> CmdStan path set to: /Users/jgabry/.cmdstan/cmdstan-2.36.0
# Create a CmdStanModel object from a Stan program,
# here using the example model that comes with CmdStan
file <- file.path(cmdstan_path(), "examples/bernoulli/bernoulli.stan")
mod <- cmdstan_model(file)
mod$print()
#> data {
#> int<lower=0> N;
#> array[N] int<lower=0, upper=1> y;
#> }
#> parameters {
#> real<lower=0, upper=1> theta;
#> }
#> model {
#> theta ~ beta(1, 1); // uniform prior on interval 0,1
#> y ~ bernoulli(theta);
#> }
# Print with line numbers. This can be set globally using the
# `cmdstanr_print_line_numbers` option.
mod$print(line_numbers = TRUE)
#> 1: data {
#> 2: int<lower=0> N;
#> 3: array[N] int<lower=0, upper=1> y;
#> 4: }
#> 5: parameters {
#> 6: real<lower=0, upper=1> theta;
#> 7: }
#> 8: model {
#> 9: theta ~ beta(1, 1); // uniform prior on interval 0,1
#> 10: y ~ bernoulli(theta);
#> 11: }
# Data as a named list (like RStan)
stan_data <- list(N = 10, y = c(0,1,0,0,0,0,0,0,0,1))
# Run MCMC using the 'sample' method
fit_mcmc <- mod$sample(
data = stan_data,
seed = 123,
chains = 2,
parallel_chains = 2
)
#> Running MCMC with 2 parallel chains...
#>
#> Chain 1 Iteration: 1 / 2000 [ 0%] (Warmup)
#> Chain 1 Iteration: 100 / 2000 [ 5%] (Warmup)
#> Chain 1 Iteration: 200 / 2000 [ 10%] (Warmup)
#> Chain 1 Iteration: 300 / 2000 [ 15%] (Warmup)
#> Chain 1 Iteration: 400 / 2000 [ 20%] (Warmup)
#> Chain 1 Iteration: 500 / 2000 [ 25%] (Warmup)
#> Chain 1 Iteration: 600 / 2000 [ 30%] (Warmup)
#> Chain 1 Iteration: 700 / 2000 [ 35%] (Warmup)
#> Chain 1 Iteration: 800 / 2000 [ 40%] (Warmup)
#> Chain 1 Iteration: 900 / 2000 [ 45%] (Warmup)
#> Chain 1 Iteration: 1000 / 2000 [ 50%] (Warmup)
#> Chain 1 Iteration: 1001 / 2000 [ 50%] (Sampling)
#> Chain 1 Iteration: 1100 / 2000 [ 55%] (Sampling)
#> Chain 1 Iteration: 1200 / 2000 [ 60%] (Sampling)
#> Chain 1 Iteration: 1300 / 2000 [ 65%] (Sampling)
#> Chain 1 Iteration: 1400 / 2000 [ 70%] (Sampling)
#> Chain 1 Iteration: 1500 / 2000 [ 75%] (Sampling)
#> Chain 1 Iteration: 1600 / 2000 [ 80%] (Sampling)
#> Chain 1 Iteration: 1700 / 2000 [ 85%] (Sampling)
#> Chain 1 Iteration: 1800 / 2000 [ 90%] (Sampling)
#> Chain 1 Iteration: 1900 / 2000 [ 95%] (Sampling)
#> Chain 1 Iteration: 2000 / 2000 [100%] (Sampling)
#> Chain 2 Iteration: 1 / 2000 [ 0%] (Warmup)
#> Chain 2 Iteration: 100 / 2000 [ 5%] (Warmup)
#> Chain 2 Iteration: 200 / 2000 [ 10%] (Warmup)
#> Chain 2 Iteration: 300 / 2000 [ 15%] (Warmup)
#> Chain 2 Iteration: 400 / 2000 [ 20%] (Warmup)
#> Chain 2 Iteration: 500 / 2000 [ 25%] (Warmup)
#> Chain 2 Iteration: 600 / 2000 [ 30%] (Warmup)
#> Chain 2 Iteration: 700 / 2000 [ 35%] (Warmup)
#> Chain 2 Iteration: 800 / 2000 [ 40%] (Warmup)
#> Chain 2 Iteration: 900 / 2000 [ 45%] (Warmup)
#> Chain 2 Iteration: 1000 / 2000 [ 50%] (Warmup)
#> Chain 2 Iteration: 1001 / 2000 [ 50%] (Sampling)
#> Chain 2 Iteration: 1100 / 2000 [ 55%] (Sampling)
#> Chain 2 Iteration: 1200 / 2000 [ 60%] (Sampling)
#> Chain 2 Iteration: 1300 / 2000 [ 65%] (Sampling)
#> Chain 2 Iteration: 1400 / 2000 [ 70%] (Sampling)
#> Chain 2 Iteration: 1500 / 2000 [ 75%] (Sampling)
#> Chain 2 Iteration: 1600 / 2000 [ 80%] (Sampling)
#> Chain 2 Iteration: 1700 / 2000 [ 85%] (Sampling)
#> Chain 2 Iteration: 1800 / 2000 [ 90%] (Sampling)
#> Chain 2 Iteration: 1900 / 2000 [ 95%] (Sampling)
#> Chain 2 Iteration: 2000 / 2000 [100%] (Sampling)
#> Chain 1 finished in 0.0 seconds.
#> Chain 2 finished in 0.0 seconds.
#>
#> Both chains finished successfully.
#> Mean chain execution time: 0.0 seconds.
#> Total execution time: 0.2 seconds.
#>
# Use 'posterior' package for summaries
fit_mcmc$summary()
#> # A tibble: 2 × 10
#> variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 lp__ -7.35 -7.01 0.882 0.353 -9.14 -6.75 1.00 724. 896.
#> 2 theta 0.254 0.239 0.129 0.126 0.0737 0.488 1.00 532. 657.
# Check sampling diagnostics
fit_mcmc$diagnostic_summary()
#> $num_divergent
#> [1] 0 0
#>
#> $num_max_treedepth
#> [1] 0 0
#>
#> $ebfmi
#> [1] 1.1148479 0.7568734
#>
# Get posterior draws
draws <- fit_mcmc$draws()
print(draws)
#> # A draws_array: 1000 iterations, 2 chains, and 2 variables
#> , , variable = lp__
#>
#> chain
#> iteration 1 2
#> 1 -7.0 -8.1
#> 2 -7.9 -7.9
#> 3 -7.4 -7.0
#> 4 -6.7 -6.8
#> 5 -6.9 -6.8
#>
#> , , variable = theta
#>
#> chain
#> iteration 1 2
#> 1 0.17 0.088
#> 2 0.46 0.097
#> 3 0.41 0.167
#> 4 0.25 0.292
#> 5 0.18 0.238
#>
#> # ... with 995 more iterations
# Convert to data frame using posterior::as_draws_df
as_draws_df(draws)
#> # A draws_df: 1000 iterations, 2 chains, and 2 variables
#> lp__ theta
#> 1 -7.0 0.17
#> 2 -7.9 0.46
#> 3 -7.4 0.41
#> 4 -6.7 0.25
#> 5 -6.9 0.18
#> 6 -6.9 0.33
#> 7 -7.2 0.15
#> 8 -6.8 0.29
#> 9 -6.8 0.24
#> 10 -6.8 0.24
#> # ... with 1990 more draws
#> # ... hidden reserved variables {'.chain', '.iteration', '.draw'}
# Plot posterior using bayesplot (ggplot2)
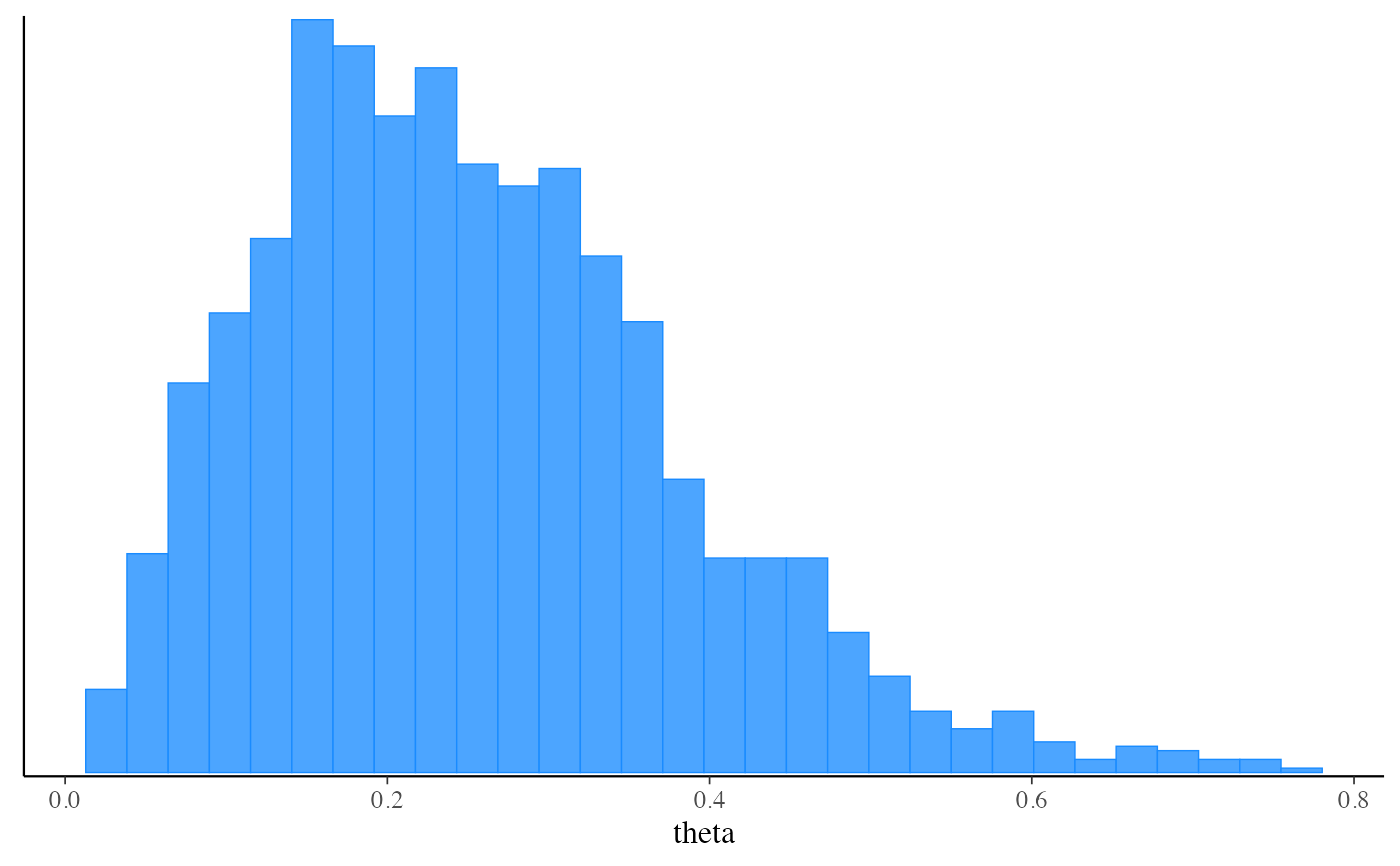
mcmc_hist(fit_mcmc$draws("theta"))
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
 # Run 'optimize' method to get a point estimate (default is Stan's LBFGS algorithm)
# and also demonstrate specifying data as a path to a file instead of a list
my_data_file <- file.path(cmdstan_path(), "examples/bernoulli/bernoulli.data.json")
fit_optim <- mod$optimize(data = my_data_file, seed = 123)
#> Initial log joint probability = -16.144
#> Iter log prob ||dx|| ||grad|| alpha alpha0 # evals Notes
#> 6 -5.00402 0.000246518 8.73164e-07 1 1 9
#> Optimization terminated normally:
#> Convergence detected: relative gradient magnitude is below tolerance
#> Finished in 0.2 seconds.
fit_optim$summary()
#> # A tibble: 2 × 2
#> variable estimate
#> <chr> <dbl>
#> 1 lp__ -5.00
#> 2 theta 0.2
# Run 'optimize' again with 'jacobian=TRUE' and then draw from Laplace approximation
# to the posterior
fit_optim <- mod$optimize(data = my_data_file, jacobian = TRUE)
#> Initial log joint probability = -19.2814
#> Iter log prob ||dx|| ||grad|| alpha alpha0 # evals Notes
#> 5 -6.74802 0.000163806 1.63613e-06 1 1 8
#> Optimization terminated normally:
#> Convergence detected: relative gradient magnitude is below tolerance
#> Finished in 0.1 seconds.
fit_laplace <- mod$laplace(data = my_data_file, mode = fit_optim, draws = 2000)
#> Calculating Hessian
#> Calculating inverse of Cholesky factor
#> Generating draws
#> iteration: 0
#> iteration: 100
#> iteration: 200
#> iteration: 300
#> iteration: 400
#> iteration: 500
#> iteration: 600
#> iteration: 700
#> iteration: 800
#> iteration: 900
#> iteration: 1000
#> iteration: 1100
#> iteration: 1200
#> iteration: 1300
#> iteration: 1400
#> iteration: 1500
#> iteration: 1600
#> iteration: 1700
#> iteration: 1800
#> iteration: 1900
#> Finished in 0.2 seconds.
fit_laplace$summary()
#> # A tibble: 3 × 7
#> variable mean median sd mad q5 q95
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 lp__ -7.24 -6.96 0.752 0.292 -8.69 -6.75
#> 2 lp_approx__ -0.496 -0.208 0.731 0.290 -1.95 -0.00172
#> 3 theta 0.270 0.248 0.123 0.116 0.0971 0.507
# Run 'variational' method to use ADVI to approximate posterior
fit_vb <- mod$variational(data = stan_data, seed = 123)
#> ------------------------------------------------------------
#> EXPERIMENTAL ALGORITHM:
#> This procedure has not been thoroughly tested and may be unstable
#> or buggy. The interface is subject to change.
#> ------------------------------------------------------------
#> Gradient evaluation took 1.1e-05 seconds
#> 1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds.
#> Adjust your expectations accordingly!
#> Begin eta adaptation.
#> Iteration: 1 / 250 [ 0%] (Adaptation)
#> Iteration: 50 / 250 [ 20%] (Adaptation)
#> Iteration: 100 / 250 [ 40%] (Adaptation)
#> Iteration: 150 / 250 [ 60%] (Adaptation)
#> Iteration: 200 / 250 [ 80%] (Adaptation)
#> Success! Found best value [eta = 1] earlier than expected.
#> Begin stochastic gradient ascent.
#> iter ELBO delta_ELBO_mean delta_ELBO_med notes
#> 100 -6.164 1.000 1.000
#> 200 -6.225 0.505 1.000
#> 300 -6.186 0.339 0.010 MEDIAN ELBO CONVERGED
#> Drawing a sample of size 1000 from the approximate posterior...
#> COMPLETED.
#> Finished in 0.2 seconds.
fit_vb$summary()
#> # A tibble: 3 × 7
#> variable mean median sd mad q5 q95
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 lp__ -7.14 -6.93 0.528 0.247 -8.21 -6.75
#> 2 lp_approx__ -0.520 -0.244 0.740 0.326 -1.90 -0.00227
#> 3 theta 0.251 0.236 0.107 0.108 0.100 0.446
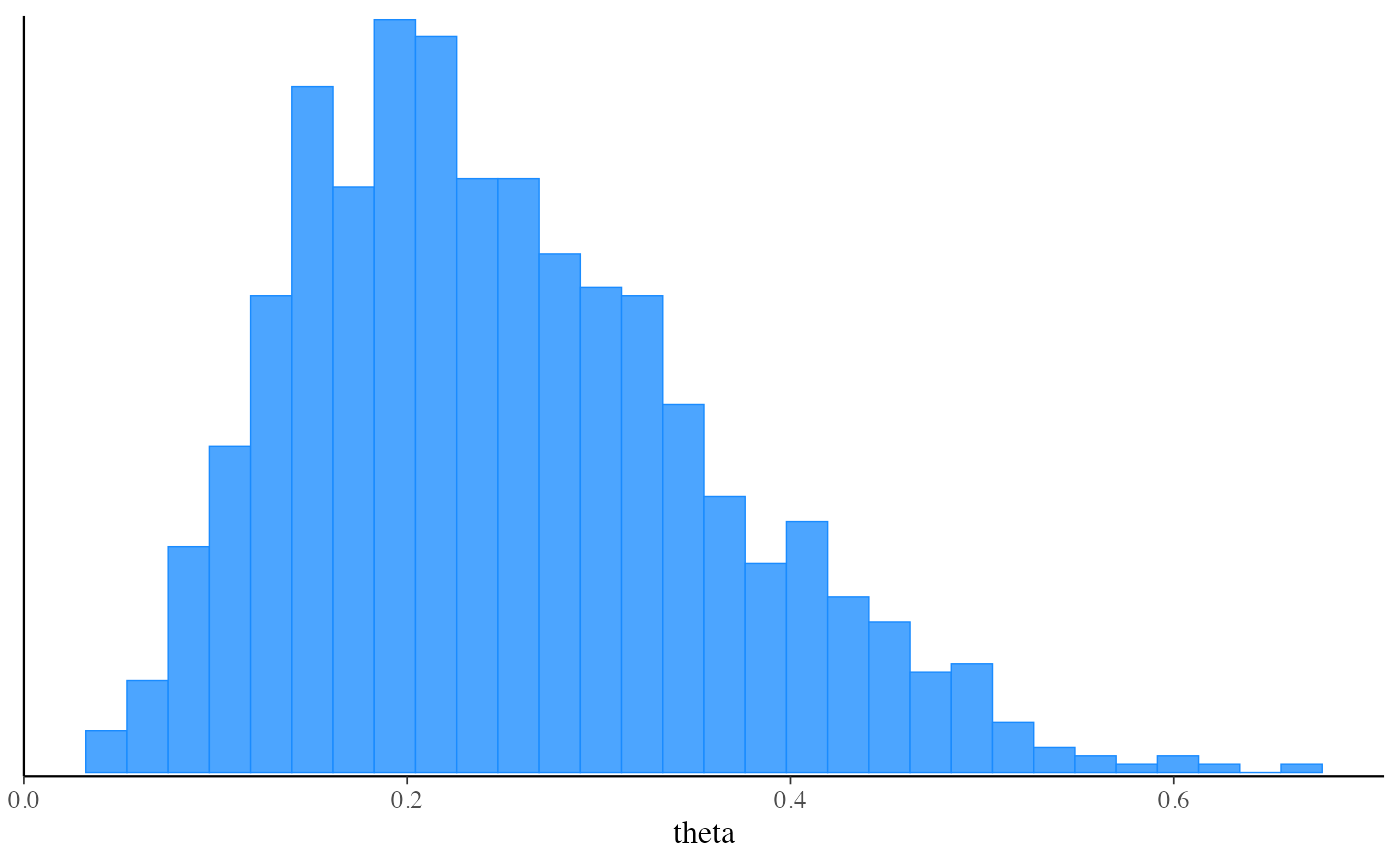
mcmc_hist(fit_vb$draws("theta"))
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
# Run 'optimize' method to get a point estimate (default is Stan's LBFGS algorithm)
# and also demonstrate specifying data as a path to a file instead of a list
my_data_file <- file.path(cmdstan_path(), "examples/bernoulli/bernoulli.data.json")
fit_optim <- mod$optimize(data = my_data_file, seed = 123)
#> Initial log joint probability = -16.144
#> Iter log prob ||dx|| ||grad|| alpha alpha0 # evals Notes
#> 6 -5.00402 0.000246518 8.73164e-07 1 1 9
#> Optimization terminated normally:
#> Convergence detected: relative gradient magnitude is below tolerance
#> Finished in 0.2 seconds.
fit_optim$summary()
#> # A tibble: 2 × 2
#> variable estimate
#> <chr> <dbl>
#> 1 lp__ -5.00
#> 2 theta 0.2
# Run 'optimize' again with 'jacobian=TRUE' and then draw from Laplace approximation
# to the posterior
fit_optim <- mod$optimize(data = my_data_file, jacobian = TRUE)
#> Initial log joint probability = -19.2814
#> Iter log prob ||dx|| ||grad|| alpha alpha0 # evals Notes
#> 5 -6.74802 0.000163806 1.63613e-06 1 1 8
#> Optimization terminated normally:
#> Convergence detected: relative gradient magnitude is below tolerance
#> Finished in 0.1 seconds.
fit_laplace <- mod$laplace(data = my_data_file, mode = fit_optim, draws = 2000)
#> Calculating Hessian
#> Calculating inverse of Cholesky factor
#> Generating draws
#> iteration: 0
#> iteration: 100
#> iteration: 200
#> iteration: 300
#> iteration: 400
#> iteration: 500
#> iteration: 600
#> iteration: 700
#> iteration: 800
#> iteration: 900
#> iteration: 1000
#> iteration: 1100
#> iteration: 1200
#> iteration: 1300
#> iteration: 1400
#> iteration: 1500
#> iteration: 1600
#> iteration: 1700
#> iteration: 1800
#> iteration: 1900
#> Finished in 0.2 seconds.
fit_laplace$summary()
#> # A tibble: 3 × 7
#> variable mean median sd mad q5 q95
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 lp__ -7.24 -6.96 0.752 0.292 -8.69 -6.75
#> 2 lp_approx__ -0.496 -0.208 0.731 0.290 -1.95 -0.00172
#> 3 theta 0.270 0.248 0.123 0.116 0.0971 0.507
# Run 'variational' method to use ADVI to approximate posterior
fit_vb <- mod$variational(data = stan_data, seed = 123)
#> ------------------------------------------------------------
#> EXPERIMENTAL ALGORITHM:
#> This procedure has not been thoroughly tested and may be unstable
#> or buggy. The interface is subject to change.
#> ------------------------------------------------------------
#> Gradient evaluation took 1.1e-05 seconds
#> 1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds.
#> Adjust your expectations accordingly!
#> Begin eta adaptation.
#> Iteration: 1 / 250 [ 0%] (Adaptation)
#> Iteration: 50 / 250 [ 20%] (Adaptation)
#> Iteration: 100 / 250 [ 40%] (Adaptation)
#> Iteration: 150 / 250 [ 60%] (Adaptation)
#> Iteration: 200 / 250 [ 80%] (Adaptation)
#> Success! Found best value [eta = 1] earlier than expected.
#> Begin stochastic gradient ascent.
#> iter ELBO delta_ELBO_mean delta_ELBO_med notes
#> 100 -6.164 1.000 1.000
#> 200 -6.225 0.505 1.000
#> 300 -6.186 0.339 0.010 MEDIAN ELBO CONVERGED
#> Drawing a sample of size 1000 from the approximate posterior...
#> COMPLETED.
#> Finished in 0.2 seconds.
fit_vb$summary()
#> # A tibble: 3 × 7
#> variable mean median sd mad q5 q95
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 lp__ -7.14 -6.93 0.528 0.247 -8.21 -6.75
#> 2 lp_approx__ -0.520 -0.244 0.740 0.326 -1.90 -0.00227
#> 3 theta 0.251 0.236 0.107 0.108 0.100 0.446
mcmc_hist(fit_vb$draws("theta"))
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
 # Run 'pathfinder' method, a new alternative to the variational method
fit_pf <- mod$pathfinder(data = stan_data, seed = 123)
#> Path [1] :Initial log joint density = -18.273334
#> Path [1] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 7.082e-04 1.432e-05 1.000e+00 1.000e+00 126 -6.145e+00 -6.145e+00
#> Path [1] :Best Iter: [5] ELBO (-6.145070) evaluations: (126)
#> Path [2] :Initial log joint density = -19.192715
#> Path [2] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 2.015e-04 2.228e-06 1.000e+00 1.000e+00 126 -6.223e+00 -6.223e+00
#> Path [2] :Best Iter: [2] ELBO (-6.170358) evaluations: (126)
#> Path [3] :Initial log joint density = -6.774820
#> Path [3] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 4 -6.748e+00 1.137e-04 2.596e-07 1.000e+00 1.000e+00 101 -6.178e+00 -6.178e+00
#> Path [3] :Best Iter: [4] ELBO (-6.177909) evaluations: (101)
#> Path [4] :Initial log joint density = -7.949193
#> Path [4] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 2.145e-04 1.301e-06 1.000e+00 1.000e+00 126 -6.197e+00 -6.197e+00
#> Path [4] :Best Iter: [5] ELBO (-6.197118) evaluations: (126)
#> Total log probability function evaluations:4379
#> Finished in 0.2 seconds.
fit_pf$summary()
#> # A tibble: 3 × 7
#> variable mean median sd mad q5 q95
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 lp_approx__ -1.07 -0.727 0.945 0.311 -2.91 -0.450
#> 2 lp__ -7.25 -6.97 0.753 0.308 -8.78 -6.75
#> 3 theta 0.256 0.245 0.119 0.123 0.0824 0.462
mcmc_hist(fit_pf$draws("theta"))
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
# Run 'pathfinder' method, a new alternative to the variational method
fit_pf <- mod$pathfinder(data = stan_data, seed = 123)
#> Path [1] :Initial log joint density = -18.273334
#> Path [1] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 7.082e-04 1.432e-05 1.000e+00 1.000e+00 126 -6.145e+00 -6.145e+00
#> Path [1] :Best Iter: [5] ELBO (-6.145070) evaluations: (126)
#> Path [2] :Initial log joint density = -19.192715
#> Path [2] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 2.015e-04 2.228e-06 1.000e+00 1.000e+00 126 -6.223e+00 -6.223e+00
#> Path [2] :Best Iter: [2] ELBO (-6.170358) evaluations: (126)
#> Path [3] :Initial log joint density = -6.774820
#> Path [3] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 4 -6.748e+00 1.137e-04 2.596e-07 1.000e+00 1.000e+00 101 -6.178e+00 -6.178e+00
#> Path [3] :Best Iter: [4] ELBO (-6.177909) evaluations: (101)
#> Path [4] :Initial log joint density = -7.949193
#> Path [4] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 2.145e-04 1.301e-06 1.000e+00 1.000e+00 126 -6.197e+00 -6.197e+00
#> Path [4] :Best Iter: [5] ELBO (-6.197118) evaluations: (126)
#> Total log probability function evaluations:4379
#> Finished in 0.2 seconds.
fit_pf$summary()
#> # A tibble: 3 × 7
#> variable mean median sd mad q5 q95
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 lp_approx__ -1.07 -0.727 0.945 0.311 -2.91 -0.450
#> 2 lp__ -7.25 -6.97 0.753 0.308 -8.78 -6.75
#> 3 theta 0.256 0.245 0.119 0.123 0.0824 0.462
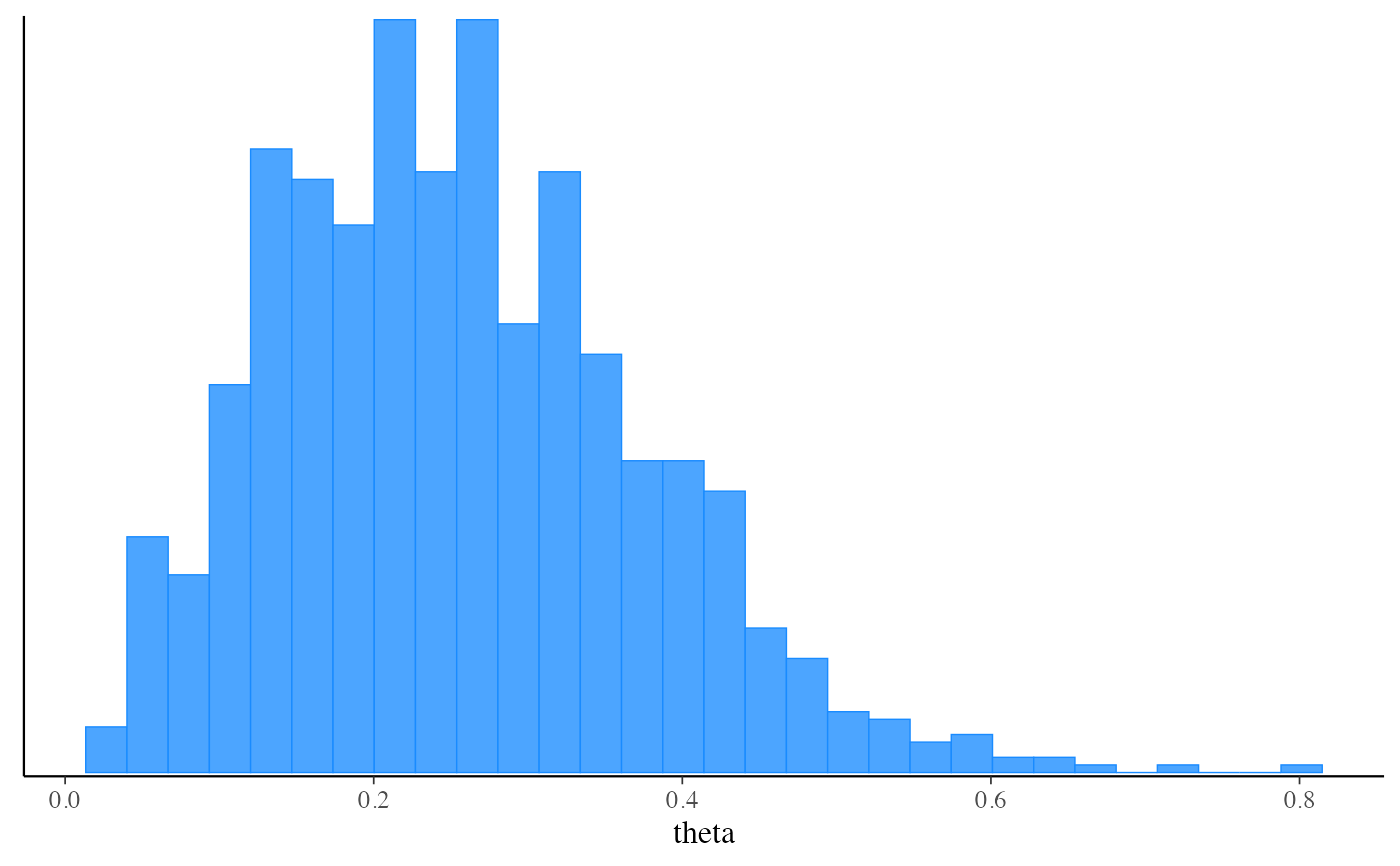
mcmc_hist(fit_pf$draws("theta"))
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
 # Run 'pathfinder' again with more paths, fewer draws per path,
# better covariance approximation, and fewer LBFGSs iterations
fit_pf <- mod$pathfinder(data = stan_data, num_paths=10, single_path_draws=40,
history_size=50, max_lbfgs_iters=100)
#> Warning: Number of PSIS draws is larger than the total number of draws returned by the single Pathfinders. This is likely unintentional and leads to re-sampling from the same draws.
#> Path [1] :Initial log joint density = -6.777948
#> Path [1] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 4 -6.748e+00 1.327e-04 3.358e-07 1.000e+00 1.000e+00 101 -6.183e+00 -6.183e+00
#> Path [1] :Best Iter: [4] ELBO (-6.183163) evaluations: (101)
#> Path [2] :Initial log joint density = -8.072775
#> Path [2] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 2.399e-04 1.562e-06 1.000e+00 1.000e+00 126 -6.271e+00 -6.271e+00
#> Path [2] :Best Iter: [4] ELBO (-6.239963) evaluations: (126)
#> Path [3] :Initial log joint density = -9.025342
#> Path [3] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 3.454e-04 2.916e-06 1.000e+00 1.000e+00 126 -6.285e+00 -6.285e+00
#> Path [3] :Best Iter: [2] ELBO (-6.207932) evaluations: (126)
#> Path [4] :Initial log joint density = -9.983004
#> Path [4] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 6.283e-04 7.448e-06 1.000e+00 1.000e+00 126 -6.267e+00 -6.267e+00
#> Path [4] :Best Iter: [3] ELBO (-6.107202) evaluations: (126)
#> Path [5] :Initial log joint density = -13.400879
#> Path [5] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 1.809e-03 4.509e-05 1.000e+00 1.000e+00 126 -6.206e+00 -6.206e+00
#> Path [5] :Best Iter: [4] ELBO (-6.199332) evaluations: (126)
#> Path [6] :Initial log joint density = -7.627321
#> Path [6] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 1.419e-04 6.650e-07 1.000e+00 1.000e+00 126 -6.197e+00 -6.197e+00
#> Path [6] :Best Iter: [4] ELBO (-6.176730) evaluations: (126)
#> Path [7] :Initial log joint density = -13.719529
#> Path [7] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 1.898e-03 4.974e-05 1.000e+00 1.000e+00 126 -6.198e+00 -6.198e+00
#> Path [7] :Best Iter: [5] ELBO (-6.198257) evaluations: (126)
#> Path [8] :Initial log joint density = -8.734378
#> Path [8] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 3.325e-04 2.705e-06 1.000e+00 1.000e+00 126 -6.215e+00 -6.215e+00
#> Path [8] :Best Iter: [3] ELBO (-6.210584) evaluations: (126)
#> Path [9] :Initial log joint density = -15.787917
#> Path [9] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 1.925e-03 5.805e-05 1.000e+00 1.000e+00 126 -6.251e+00 -6.251e+00
#> Path [9] :Best Iter: [3] ELBO (-6.246013) evaluations: (126)
#> Path [10] :Initial log joint density = -7.311648
#> Path [10] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 4 -6.748e+00 5.348e-03 1.585e-04 1.000e+00 1.000e+00 101 -6.229e+00 -6.229e+00
#> Path [10] :Best Iter: [3] ELBO (-6.203261) evaluations: (101)
#> Total log probability function evaluations:1360
#> Pareto k value (0.78) is greater than 0.7. Importance resampling was not able to improve the approximation, which may indicate that the approximation itself is poor.
#> Finished in 0.2 seconds.
# Specifying initial values as a function
fit_mcmc_w_init_fun <- mod$sample(
data = stan_data,
seed = 123,
chains = 2,
refresh = 0,
init = function() list(theta = runif(1))
)
#> Running MCMC with 2 sequential chains...
#>
#> Chain 1 finished in 0.0 seconds.
#> Chain 2 finished in 0.0 seconds.
#>
#> Both chains finished successfully.
#> Mean chain execution time: 0.0 seconds.
#> Total execution time: 0.4 seconds.
#>
fit_mcmc_w_init_fun_2 <- mod$sample(
data = stan_data,
seed = 123,
chains = 2,
refresh = 0,
init = function(chain_id) {
# silly but demonstrates optional use of chain_id
list(theta = 1 / (chain_id + 1))
}
)
#> Running MCMC with 2 sequential chains...
#>
#> Chain 1 finished in 0.0 seconds.
#> Chain 2 finished in 0.0 seconds.
#>
#> Both chains finished successfully.
#> Mean chain execution time: 0.0 seconds.
#> Total execution time: 0.3 seconds.
#>
fit_mcmc_w_init_fun_2$init()
#> [[1]]
#> [[1]]$theta
#> [1] 0.5
#>
#>
#> [[2]]
#> [[2]]$theta
#> [1] 0.3333333
#>
#>
# Specifying initial values as a list of lists
fit_mcmc_w_init_list <- mod$sample(
data = stan_data,
seed = 123,
chains = 2,
refresh = 0,
init = list(
list(theta = 0.75), # chain 1
list(theta = 0.25) # chain 2
)
)
#> Running MCMC with 2 sequential chains...
#>
#> Chain 1 finished in 0.0 seconds.
#> Chain 2 finished in 0.0 seconds.
#>
#> Both chains finished successfully.
#> Mean chain execution time: 0.0 seconds.
#> Total execution time: 0.3 seconds.
#>
fit_optim_w_init_list <- mod$optimize(
data = stan_data,
seed = 123,
init = list(
list(theta = 0.75)
)
)
#> Initial log joint probability = -11.6657
#> Iter log prob ||dx|| ||grad|| alpha alpha0 # evals Notes
#> 6 -5.00402 0.000237915 9.55309e-07 1 1 9
#> Optimization terminated normally:
#> Convergence detected: relative gradient magnitude is below tolerance
#> Finished in 0.2 seconds.
fit_optim_w_init_list$init()
#> [[1]]
#> [[1]]$theta
#> [1] 0.75
#>
#>
# }
# Run 'pathfinder' again with more paths, fewer draws per path,
# better covariance approximation, and fewer LBFGSs iterations
fit_pf <- mod$pathfinder(data = stan_data, num_paths=10, single_path_draws=40,
history_size=50, max_lbfgs_iters=100)
#> Warning: Number of PSIS draws is larger than the total number of draws returned by the single Pathfinders. This is likely unintentional and leads to re-sampling from the same draws.
#> Path [1] :Initial log joint density = -6.777948
#> Path [1] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 4 -6.748e+00 1.327e-04 3.358e-07 1.000e+00 1.000e+00 101 -6.183e+00 -6.183e+00
#> Path [1] :Best Iter: [4] ELBO (-6.183163) evaluations: (101)
#> Path [2] :Initial log joint density = -8.072775
#> Path [2] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 2.399e-04 1.562e-06 1.000e+00 1.000e+00 126 -6.271e+00 -6.271e+00
#> Path [2] :Best Iter: [4] ELBO (-6.239963) evaluations: (126)
#> Path [3] :Initial log joint density = -9.025342
#> Path [3] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 3.454e-04 2.916e-06 1.000e+00 1.000e+00 126 -6.285e+00 -6.285e+00
#> Path [3] :Best Iter: [2] ELBO (-6.207932) evaluations: (126)
#> Path [4] :Initial log joint density = -9.983004
#> Path [4] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 6.283e-04 7.448e-06 1.000e+00 1.000e+00 126 -6.267e+00 -6.267e+00
#> Path [4] :Best Iter: [3] ELBO (-6.107202) evaluations: (126)
#> Path [5] :Initial log joint density = -13.400879
#> Path [5] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 1.809e-03 4.509e-05 1.000e+00 1.000e+00 126 -6.206e+00 -6.206e+00
#> Path [5] :Best Iter: [4] ELBO (-6.199332) evaluations: (126)
#> Path [6] :Initial log joint density = -7.627321
#> Path [6] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 1.419e-04 6.650e-07 1.000e+00 1.000e+00 126 -6.197e+00 -6.197e+00
#> Path [6] :Best Iter: [4] ELBO (-6.176730) evaluations: (126)
#> Path [7] :Initial log joint density = -13.719529
#> Path [7] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 1.898e-03 4.974e-05 1.000e+00 1.000e+00 126 -6.198e+00 -6.198e+00
#> Path [7] :Best Iter: [5] ELBO (-6.198257) evaluations: (126)
#> Path [8] :Initial log joint density = -8.734378
#> Path [8] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 3.325e-04 2.705e-06 1.000e+00 1.000e+00 126 -6.215e+00 -6.215e+00
#> Path [8] :Best Iter: [3] ELBO (-6.210584) evaluations: (126)
#> Path [9] :Initial log joint density = -15.787917
#> Path [9] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 5 -6.748e+00 1.925e-03 5.805e-05 1.000e+00 1.000e+00 126 -6.251e+00 -6.251e+00
#> Path [9] :Best Iter: [3] ELBO (-6.246013) evaluations: (126)
#> Path [10] :Initial log joint density = -7.311648
#> Path [10] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 4 -6.748e+00 5.348e-03 1.585e-04 1.000e+00 1.000e+00 101 -6.229e+00 -6.229e+00
#> Path [10] :Best Iter: [3] ELBO (-6.203261) evaluations: (101)
#> Total log probability function evaluations:1360
#> Pareto k value (0.78) is greater than 0.7. Importance resampling was not able to improve the approximation, which may indicate that the approximation itself is poor.
#> Finished in 0.2 seconds.
# Specifying initial values as a function
fit_mcmc_w_init_fun <- mod$sample(
data = stan_data,
seed = 123,
chains = 2,
refresh = 0,
init = function() list(theta = runif(1))
)
#> Running MCMC with 2 sequential chains...
#>
#> Chain 1 finished in 0.0 seconds.
#> Chain 2 finished in 0.0 seconds.
#>
#> Both chains finished successfully.
#> Mean chain execution time: 0.0 seconds.
#> Total execution time: 0.4 seconds.
#>
fit_mcmc_w_init_fun_2 <- mod$sample(
data = stan_data,
seed = 123,
chains = 2,
refresh = 0,
init = function(chain_id) {
# silly but demonstrates optional use of chain_id
list(theta = 1 / (chain_id + 1))
}
)
#> Running MCMC with 2 sequential chains...
#>
#> Chain 1 finished in 0.0 seconds.
#> Chain 2 finished in 0.0 seconds.
#>
#> Both chains finished successfully.
#> Mean chain execution time: 0.0 seconds.
#> Total execution time: 0.3 seconds.
#>
fit_mcmc_w_init_fun_2$init()
#> [[1]]
#> [[1]]$theta
#> [1] 0.5
#>
#>
#> [[2]]
#> [[2]]$theta
#> [1] 0.3333333
#>
#>
# Specifying initial values as a list of lists
fit_mcmc_w_init_list <- mod$sample(
data = stan_data,
seed = 123,
chains = 2,
refresh = 0,
init = list(
list(theta = 0.75), # chain 1
list(theta = 0.25) # chain 2
)
)
#> Running MCMC with 2 sequential chains...
#>
#> Chain 1 finished in 0.0 seconds.
#> Chain 2 finished in 0.0 seconds.
#>
#> Both chains finished successfully.
#> Mean chain execution time: 0.0 seconds.
#> Total execution time: 0.3 seconds.
#>
fit_optim_w_init_list <- mod$optimize(
data = stan_data,
seed = 123,
init = list(
list(theta = 0.75)
)
)
#> Initial log joint probability = -11.6657
#> Iter log prob ||dx|| ||grad|| alpha alpha0 # evals Notes
#> 6 -5.00402 0.000237915 9.55309e-07 1 1 9
#> Optimization terminated normally:
#> Convergence detected: relative gradient magnitude is below tolerance
#> Finished in 0.2 seconds.
fit_optim_w_init_list$init()
#> [[1]]
#> [[1]]$theta
#> [1] 0.75
#>
#>
# }