Calculate R* convergence diagnostic

The rstar() function generates a measure of convergence for MCMC draws based on whether it is possible to determine the Markov chain that generated a draw with probability greater than chance. To do so, it fits a machine learning classifier to a training set of MCMC draws and evaluates its predictive accuracy on a testing set: giving the ratio of accuracy to predicting a chain uniformly at random.

rstar(
  x,
  split = TRUE,
  uncertainty = FALSE,
  method = "rf",
  hyperparameters = NULL,
  training_proportion = 0.7,
  nsimulations = 1000,
  ...
)

Arguments

x: (draws) A draws_df object or one coercible to a draws_df object.
split: (logical) Should the estimate be computed on split chains? The default is TRUE.
uncertainty: (logical). Indicates whether to provide a vector of R* values representing uncertainty in the calculated value (if TRUE) or a single value (if FALSE). The default is TRUE.
method: (string) The machine learning classifier to use (must be available in the caret package). The default is "rf", which calls the random forest classifier.
hyperparameters: (named list) Hyperparameter settings passed to the classifier. The default for the random forest classifier (method = "rf") is list(mtry = floor(sqt(nvariables(x)))). The default for the gradient-based model (method = "gbm") is list(interaction.depth = 3, n.trees = 50, shrinkage = 0.1, n.minobsinnode = 10).
training_proportion: (positive real) The proportion (in (0,1)) of iterations in used to train the classifier. The default is 0.7.
nsimulations: (positive integer) The number of R* values in the returned vector if uncertainty is TRUE. The default is 1000.
...: Other arguments passed to caret::train().

Value

A numeric vector of length 1 (by default) or length nsimulations

(if uncertainty = TRUE).

Details

The rstar() function provides a measure of MCMC convergence based on whether it is possible to determine the chain that generated a particular draw with a probability greater than chance. To do so, it fits a machine learning classifier to a subset of the original MCMC draws (the training set) and evaluates its predictive accuracy on the remaining draws (the testing set). If predictive accuracy exceeds chance (i.e. predicting the chain that generated a draw uniformly at random), the diagnostic measure R* will be above 1, indicating that convergence has yet to occur. This statistic is recently developed, and it is currently unclear what is a reasonable threshold for diagnosing convergence.

The statistic, R*, is stochastic, meaning that each time the test is run, unless the random seed is fixed, it will generally produce a different result. To minimize the implications of this stochasticity, it is recommended to repeatedly run this function to calculate a distribution of R*; alternatively, an approximation to this distribution can be obtained by setting uncertainty = TRUE, although this approximation of uncertainty will generally have a lower mean.

By default, a random forest classifier is used (method = "rf"), which tends to perform best for target distributions of around 4 dimensions and above. For lower dimensional targets, gradient boosted models (called via method = "gbm") tend to have a higher classification accuracy. On a given MCMC sample, it is recommended to try both of these classifiers.

References

Ben Lambert, Aki Vehtari (2020) R*: A robust MCMC convergence diagnostic with uncertainty using gradient-boosted machines. arXiv preprint arXiv:2003.07900.

Examples

# \donttest{
if (require("caret", quietly = TRUE) && require("randomForest", quietly = TRUE)) {
  x <- example_draws("eight_schools")
  print(rstar(x))
  print(rstar(x, split = FALSE))
  print(rstar(x, method = "gbm"))
  # can pass additional arguments to methods
  print(rstar(x, method = "gbm", verbose = FALSE))

  # with uncertainty, returns a vector of R* values
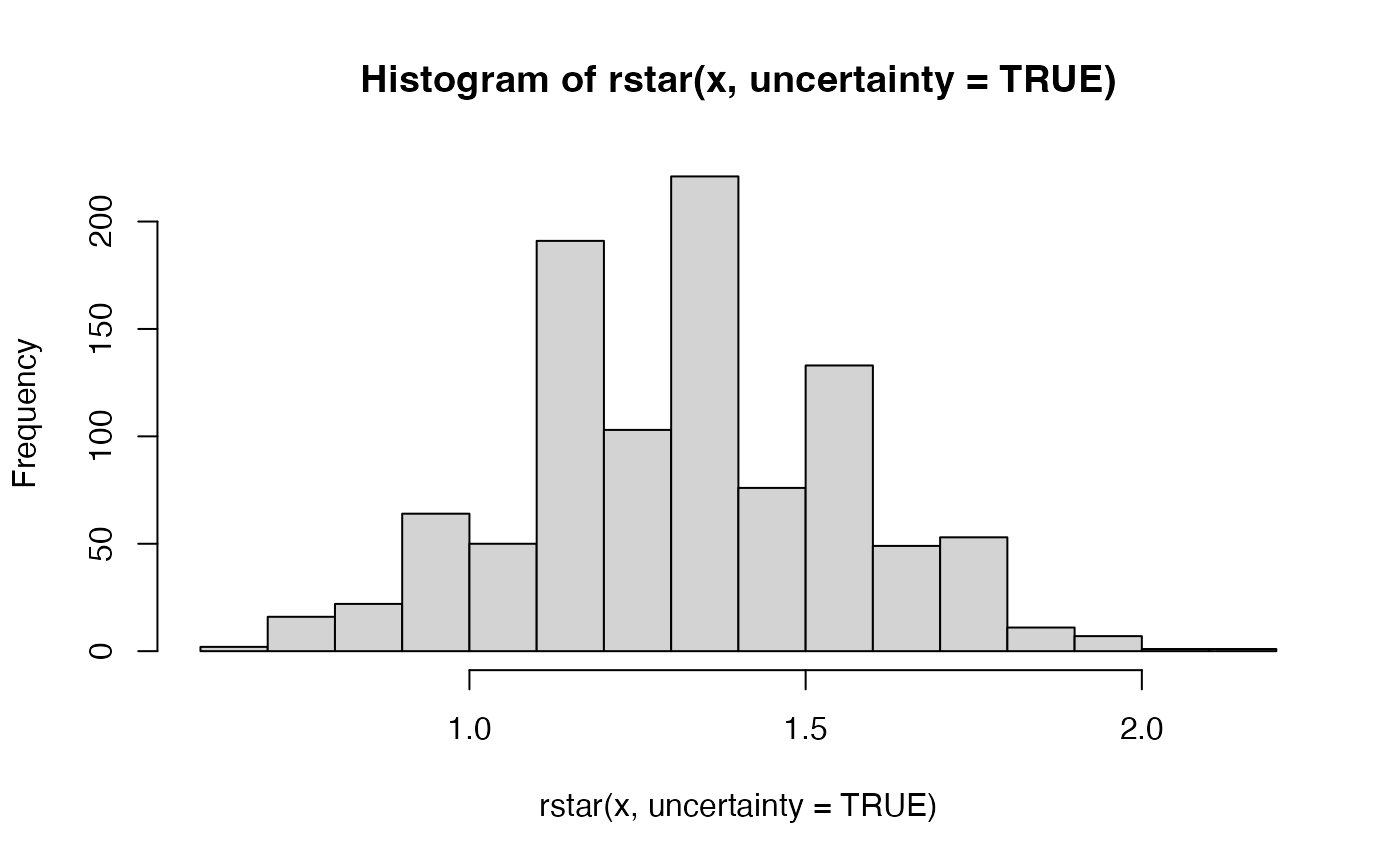
  hist(rstar(x, uncertainty = TRUE))
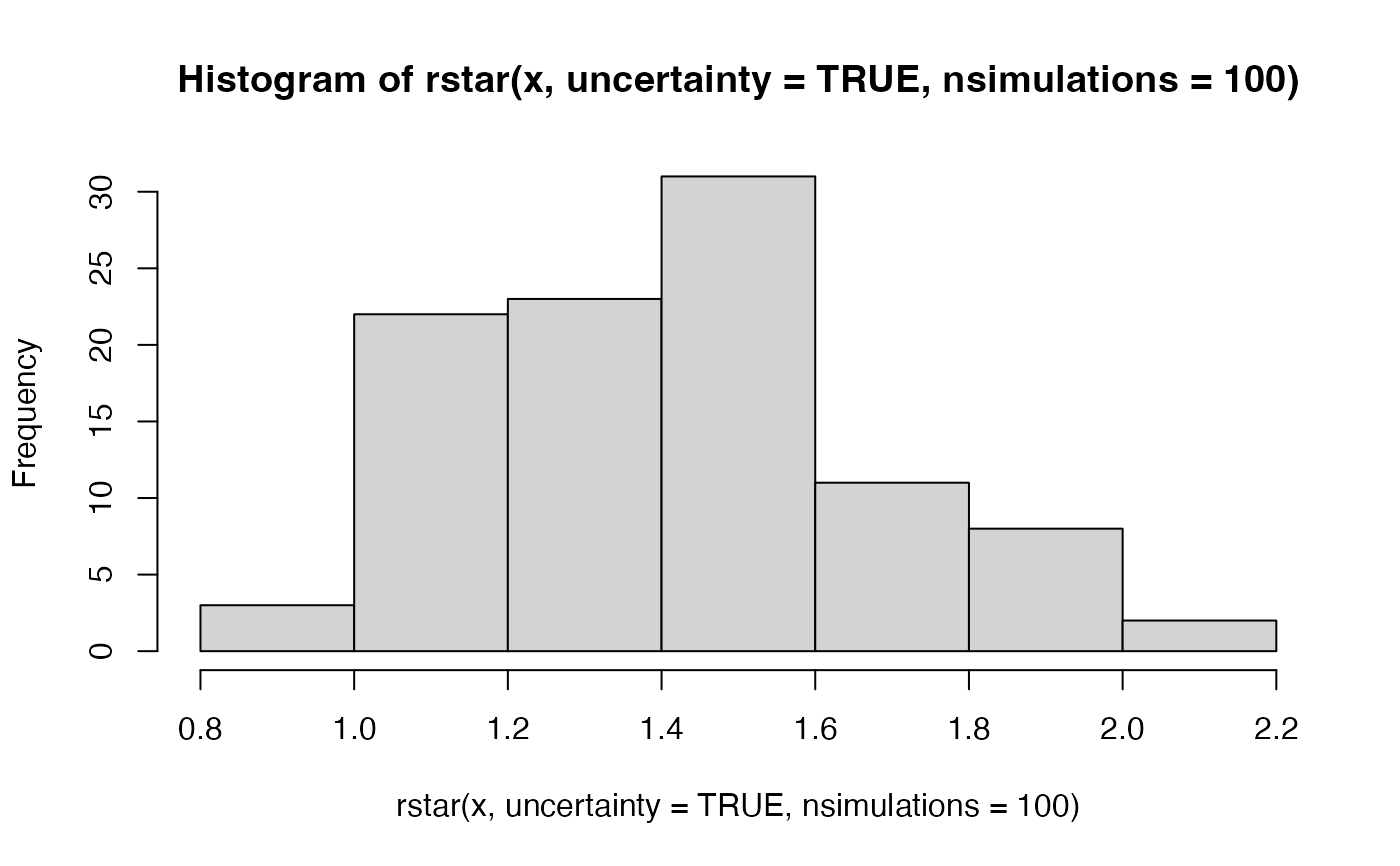
  hist(rstar(x, uncertainty = TRUE, nsimulations = 100))

  # can use other classification methods in caret library
  print(rstar(x, method = "knn"))
}
#> Warning: package ‘ggplot2’ was built under R version 4.2.3
#> randomForest 4.7-1.1
#> Type rfNews() to see new features/changes/bug fixes.
#> 
#> Attaching package: ‘randomForest’
#> The following object is masked from ‘package:ggplot2’:
#> 
#>     margin
#> [1] 1.866667
#> [1] 1.333333
#> Iter   TrainDeviance   ValidDeviance   StepSize   Improve
#>      1        2.0794             nan     0.1000   -0.0009
#>      2        2.0070             nan     0.1000   -0.0016
#>      3        1.9411             nan     0.1000   -0.0005
#>      4        1.8763             nan     0.1000   -0.0296
#>      5        1.8258             nan     0.1000   -0.0062
#>      6        1.7644             nan     0.1000   -0.0023
#>      7        1.7046             nan     0.1000   -0.0611
#>      8        1.6626             nan     0.1000   -0.0475
#>      9        1.6209             nan     0.1000   -0.0613
#>     10        1.5857             nan     0.1000   -0.0108
#>     20        1.2606             nan     0.1000   -0.0210
#>     40        0.8717             nan     0.1000   -0.0412
#>     50        0.7334             nan     0.1000   -0.0256
#> 
#> [1] 1.466667
#> [1] 1.466667


#> [1] 1.4
# }