Pareto smoothed importance sampling (PSIS)

Implementation of Pareto smoothed importance sampling (PSIS), a method for stabilizing importance ratios. The version of PSIS implemented here corresponds to the algorithm presented in Vehtari, Simpson, Gelman, Yao, and Gabry (2019). For PSIS diagnostics see the pareto-k-diagnostic page.

psis(log_ratios, ...)

# S3 method for array
psis(log_ratios, ..., r_eff = NULL, cores = getOption("mc.cores", 1))

# S3 method for matrix
psis(log_ratios, ..., r_eff = NULL, cores = getOption("mc.cores", 1))

# S3 method for default
psis(log_ratios, ..., r_eff = NULL)

is.psis(x)

is.sis(x)

is.tis(x)

Arguments

log_ratios	An array, matrix, or vector of importance ratios on the log scale (for PSIS-LOO these are negative log-likelihood values). See the Methods (by class) section below for a detailed description of how to specify the inputs for each method.
...	Arguments passed on to the various methods.
r_eff	Vector of relative effective sample size estimates containing one element per observation. The values provided should be the relative effective sample sizes of 1/exp(log_ratios) (i.e., 1/ratios). This is related to the relative efficiency of estimating the normalizing term in self-normalizing importance sampling. If r_eff is not provided then the reported PSIS effective sample sizes and Monte Carlo error estimates will be over-optimistic. See the relative_eff() helper function for computing r_eff. If using psis with draws of the log_ratios not obtained from MCMC then the warning message thrown when not specifying r_eff can be disabled by setting r_eff to NA.
cores	The number of cores to use for parallelization. This defaults to the option mc.cores which can be set for an entire R session by options(mc.cores = NUMBER). The old option loo.cores is now deprecated but will be given precedence over mc.cores until loo.cores is removed in a future release. As of version 2.0.0 the default is now 1 core if mc.cores is not set, but we recommend using as many (or close to as many) cores as possible. Note for Windows 10 users: it is strongly recommended to avoid using the .Rprofile file to set mc.cores (using the cores argument or setting mc.cores interactively or in a script is fine).
x	For is.psis(), an object to check.

Value

The psis() methods return an object of class "psis", which is a named list with the following components:

log_weights

Vector or matrix of smoothed (and truncated) but unnormalized log weights. To get normalized weights use the weights() method provided for objects of class "psis".

diagnostics

A named list containing two vectors:

• pareto_k: Estimates of the shape parameter \(k\) of the generalized Pareto distribution. See the pareto-k-diagnostic page for details.

• n_eff: PSIS effective sample size estimates.

Objects of class "psis" also have the following attributes:

norm_const_log

Vector of precomputed values of colLogSumExps(log_weights) that are used internally by the weights method to normalize the log weights.

tail_len

Vector of tail lengths used for fitting the generalized Pareto distribution.

r_eff

If specified, the user's r_eff argument.

dims

Integer vector of length 2 containing S (posterior sample size) and N (number of observations).

method

Method used for importance sampling, here psis.

Methods (by class)

• array: An \(I\) by \(C\) by \(N\) array, where \(I\) is the number of MCMC iterations per chain, \(C\) is the number of chains, and \(N\) is the number of data points.

• matrix: An \(S\) by \(N\) matrix, where \(S\) is the size of the posterior sample (with all chains merged) and \(N\) is the number of data points.

• default: A vector of length \(S\) (posterior sample size).

References

Vehtari, A., Gelman, A., and Gabry, J. (2017a). Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Statistics and Computing. 27(5), 1413--1432. doi:10.1007/s11222-016-9696-4 (journal version, preprint arXiv:1507.04544).

Vehtari, A., Simpson, D., Gelman, A., Yao, Y., and Gabry, J. (2019). Pareto smoothed importance sampling. preprint arXiv:1507.02646

See also

• loo() for approximate LOO-CV using PSIS.

• pareto-k-diagnostic for PSIS diagnostics.

Examples

log_ratios <- -1 * example_loglik_array()
r_eff <- relative_eff(exp(-log_ratios))
psis_result <- psis(log_ratios, r_eff = r_eff)
str(psis_result)
#> List of 2
#>  $ log_weights: num [1:1000, 1:32] 2.37 2.12 2.24 2.41 2.25 ...
#>  $ diagnostics:List of 2
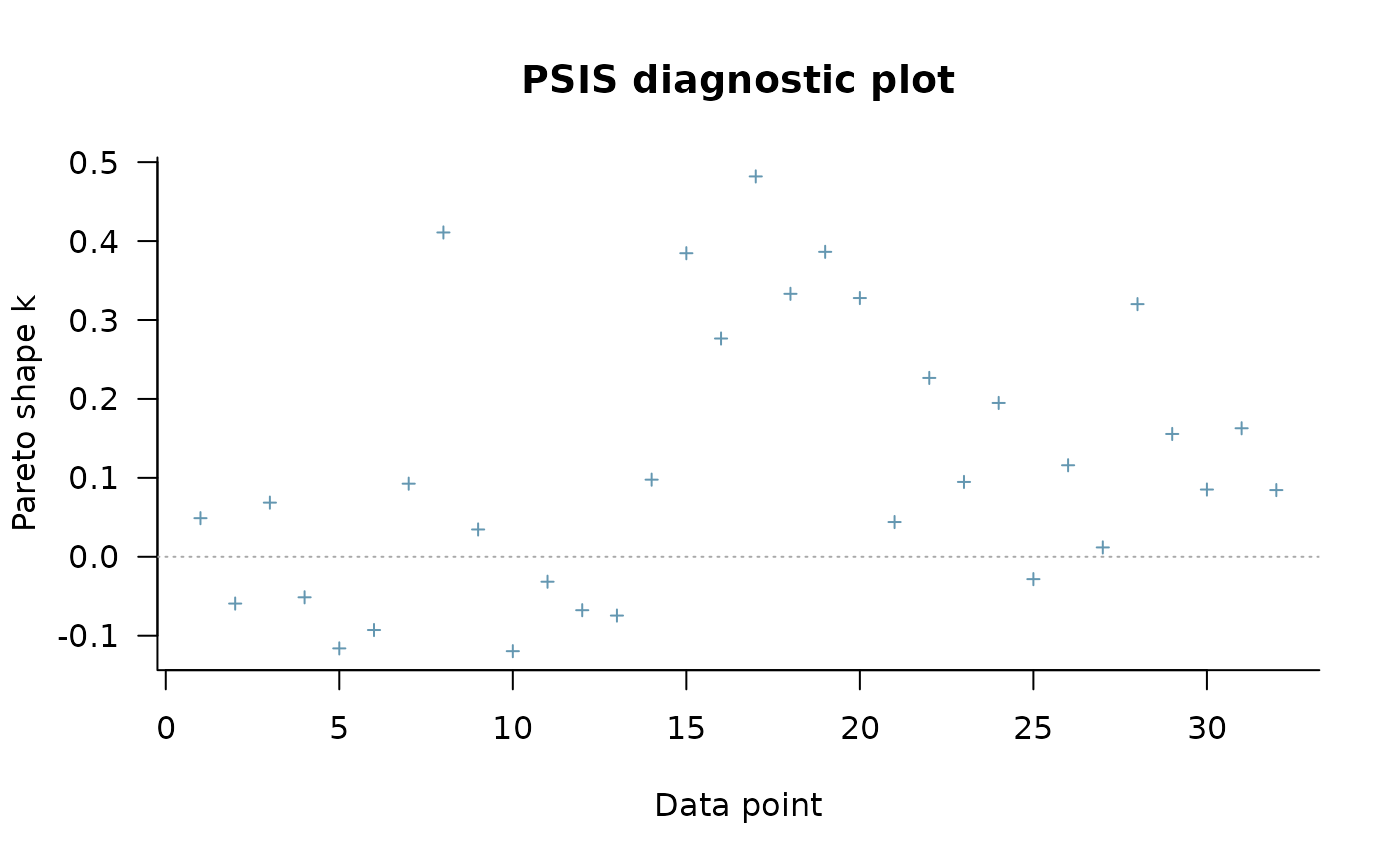
#>   ..$ pareto_k: num [1:32] 0.0447 -0.0593 0.0696 -0.052 -0.1159 ...
#>   ..$ n_eff   : num [1:32] 901 923 929 896 895 ...
#>  - attr(*, "norm_const_log")= num [1:32] 9.28 9.04 9.25 9.09 9 ...
#>  - attr(*, "tail_len")= num [1:32] 99 98 97 100 100 102 99 100 103 98 ...
#>  - attr(*, "r_eff")= num [1:32] 0.933 0.939 0.968 0.913 0.911 ...
#>  - attr(*, "dims")= int [1:2] 1000 32
#>  - attr(*, "method")= chr "psis"
#>  - attr(*, "class")= chr [1:3] "psis" "importance_sampling" "list"
plot(psis_result)

# extract smoothed weights
lw <- weights(psis_result) # default args are log=TRUE, normalize=TRUE
ulw <- weights(psis_result, normalize=FALSE) # unnormalized log-weights

w <- weights(psis_result, log=FALSE) # normalized weights (not log-weights)
uw <- weights(psis_result, log=FALSE, normalize = FALSE) # unnormalized weights