Parallel coordinates plot of MCMC draws

Parallel coordinates plot of MCMC draws (one dimension per parameter). See the Plot Descriptions section below for details, and see Gabry et al. (2019) for more background and a real example.

mcmc_parcoord(
  x,
  pars = character(),
  regex_pars = character(),
  transformations = list(),
  ...,
  size = 0.2,
  alpha = 0.3,
  np = NULL,
  np_style = parcoord_style_np()
)

mcmc_parcoord_data(
  x,
  pars = character(),
  regex_pars = character(),
  transformations = list(),
  np = NULL
)

parcoord_style_np(div_color = "red", div_size = 0.2, div_alpha = 0.2)

Arguments

x

An object containing MCMC draws:

A 3-D array, matrix, list of matrices, or data frame. The MCMC-overview page provides details on how to specify each these.
A draws object from the posterior package (e.g., draws_array, draws_rvars, etc.).
An object with an as.array() method that returns the same kind of 3-D array described on the MCMC-overview page.

pars

An optional character vector of parameter names. If neither pars nor regex_pars is specified then the default is to use all parameters. As of version 1.7.0, bayesplot also supports 'tidy' parameter selection by specifying pars = vars(...), where ... is specified the same way as in dplyr::select(...) and similar functions. Examples of using pars in this way can be found on the Tidy parameter selection page.

regex_pars

An optional regular expression to use for parameter selection. Can be specified instead of pars or in addition to pars. When using pars for tidy parameter selection, the regex_pars argument is ignored since select helpers perform a similar function.

transformations

Optionally, transformations to apply to parameters before plotting. If transformations is a function or a single string naming a function then that function will be used to transform all parameters. To apply transformations to particular parameters, the transformations argument can be a named list with length equal to the number of parameters to be transformed. Currently only univariate transformations of scalar parameters can be specified (multivariate transformations will be implemented in a future release). If transformations is a list, the name of each list element should be a parameter name and the content of each list element should be a function (or any item to match as a function via match.fun(), e.g. a string naming a function). If a function is specified by its name as a string (e.g. "log"), then it can be used to construct a new parameter label for the appropriate parameter (e.g. "log(sigma)"). If a function itself is specified (e.g. log or function(x) log(x)) then "t" is used in the new parameter label to indicate that the parameter is transformed (e.g. "t(sigma)").

Note: due to partial argument matching transformations can be abbreviated for convenience in interactive use (e.g., transform).

...

Currently ignored.

size, alpha

Arguments passed on to ggplot2::geom_line().

np

For models fit using NUTS (more generally, any symplectic integrator), an optional data frame providing NUTS diagnostic information. The data frame should be the object returned by nuts_params() or one with the same structure.

np_style

A call to the parcoord_style_np() helper function to specify arguments controlling the appearance of superimposed lines representing NUTS diagnostics (in this case divergences) if the np argument is specified.

div_color, div_size, div_alpha

Optional arguments to the parcoord_style_np() helper function that are eventually passed to ggplot2::geom_line() if the np argument is also specified. They control the color, size, and transparency specifications for showing divergences in the plot. The default values are displayed in the Usage section above.

Value

The plotting functions return a ggplot object that can be further customized using the ggplot2 package. The functions with suffix _data() return the data that would have been drawn by the plotting function.

Plot Descriptions

mcmc_parcoord()

Parallel coordinates plot of MCMC draws. There is one dimension per parameter along the horizontal axis and each set of connected line segments represents a single MCMC draw (i.e., a vector of length equal to the number of parameters).

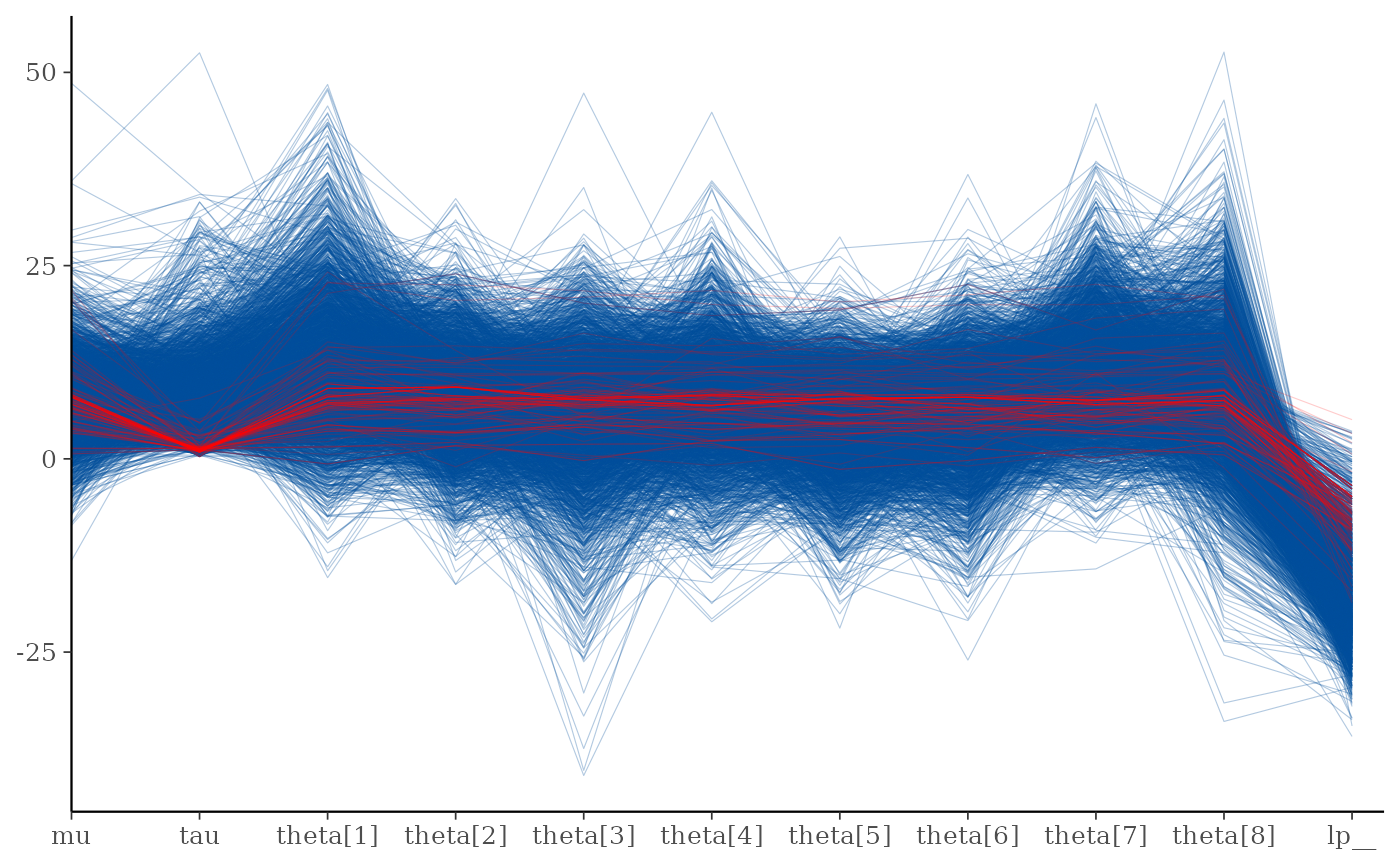
The parallel coordinates plot is most useful if the optional HMC/NUTS diagnostic information is provided via the np argument. In that case divergences are highlighted in the plot. The appearance of the divergences can be customized using the np_style argument and the parcoord_style_np helper function. This version of the plot is the same as the parallel coordinates plot described in Gabry et al. (2019).

When the plotted model parameters are on very different scales the transformations argument can be useful. For example, to standardize all variables before plotting you could use function (x - mean(x))/sd(x) when specifying the transformations argument to mcmc_parcoord. See the Examples section for how to do this.

References

Gabry, J. , Simpson, D. , Vehtari, A. , Betancourt, M. and Gelman, A. (2019), Visualization in Bayesian workflow. J. R. Stat. Soc. A, 182: 389-402. doi:10.1111/rssa.12378. (journal version, arXiv preprint, code on GitHub)

Hartikainen, A. (2017, Aug 23). Concentration of divergences (Msg 21). Message posted to The Stan Forums: https://discourse.mc-stan.org/t/concentration-of-divergences/1590/21.

Examples

color_scheme_set("pink")
x <- example_mcmc_draws(params = 5)
mcmc_parcoord(x)

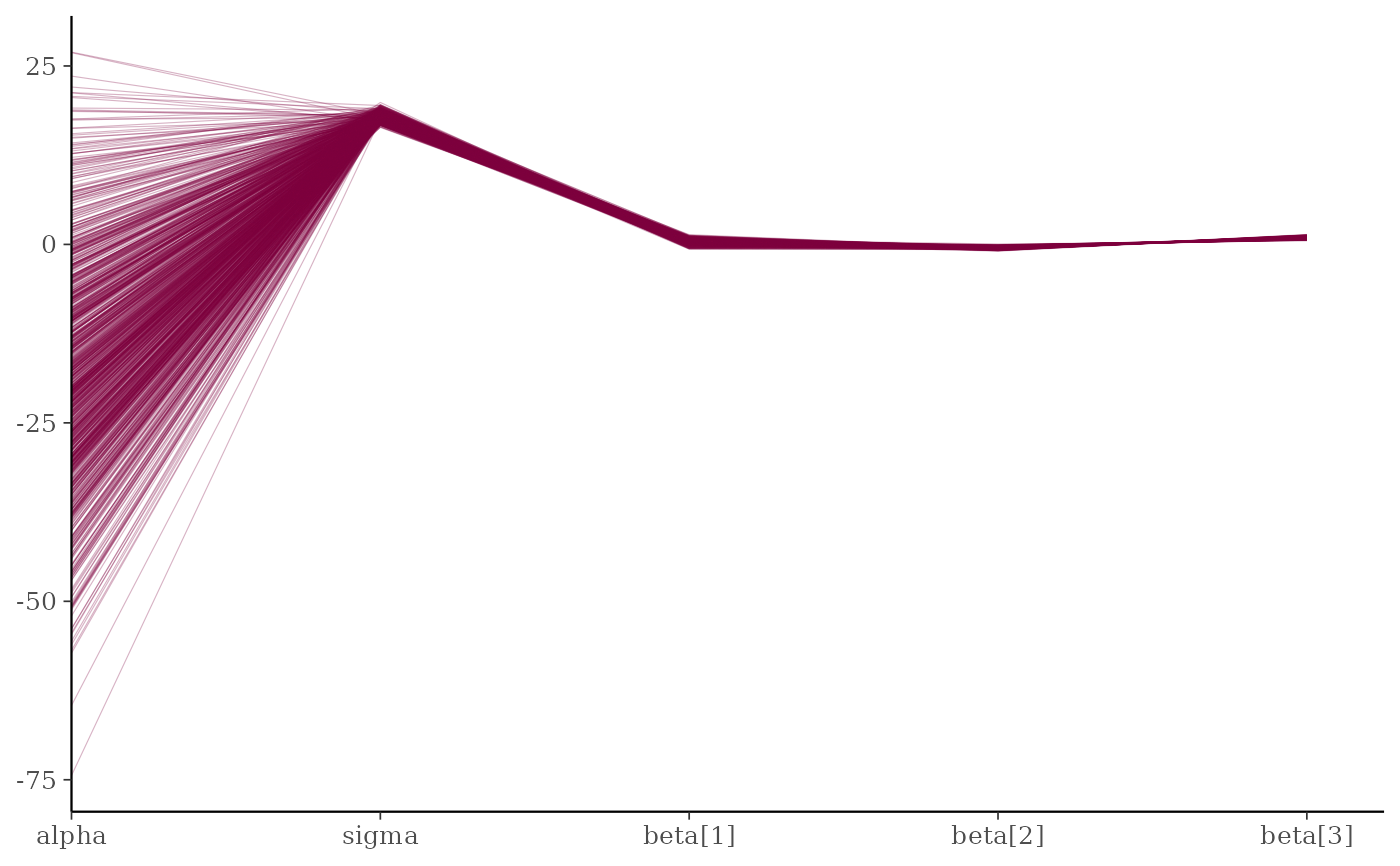mcmc_parcoord(x, regex_pars = "beta")


# \dontrun{
# Example using a Stan demo model
library(rstan)
#> Loading required package: StanHeaders
#> 
#> rstan version 2.32.3 (Stan version 2.26.1)
#> For execution on a local, multicore CPU with excess RAM we recommend calling
#> options(mc.cores = parallel::detectCores()).
#> To avoid recompilation of unchanged Stan programs, we recommend calling
#> rstan_options(auto_write = TRUE)
#> For within-chain threading using `reduce_sum()` or `map_rect()` Stan functions,
#> change `threads_per_chain` option:
#> rstan_options(threads_per_chain = 1)
fit <- stan_demo("eight_schools")
#> 
#> > J <- 8
#> 
#> > y <- c(28, 8, -3, 7, -1, 1, 18, 12)
#> 
#> > sigma <- c(15, 10, 16, 11, 9, 11, 10, 18)
#> 
#> > tau <- 25
#> 
#> SAMPLING FOR MODEL 'eight_schools' NOW (CHAIN 1).
#> Chain 1: 
#> Chain 1: Gradient evaluation took 2e-05 seconds
#> Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.2 seconds.
#> Chain 1: Adjust your expectations accordingly!
#> Chain 1: 
#> Chain 1: 
#> Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 1: 
#> Chain 1:  Elapsed Time: 0.104 seconds (Warm-up)
#> Chain 1:                0.071 seconds (Sampling)
#> Chain 1:                0.175 seconds (Total)
#> Chain 1: 
#> 
#> SAMPLING FOR MODEL 'eight_schools' NOW (CHAIN 2).
#> Chain 2: 
#> Chain 2: Gradient evaluation took 4e-06 seconds
#> Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.04 seconds.
#> Chain 2: Adjust your expectations accordingly!
#> Chain 2: 
#> Chain 2: 
#> Chain 2: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 2: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 2: 
#> Chain 2:  Elapsed Time: 0.09 seconds (Warm-up)
#> Chain 2:                0.073 seconds (Sampling)
#> Chain 2:                0.163 seconds (Total)
#> Chain 2: 
#> 
#> SAMPLING FOR MODEL 'eight_schools' NOW (CHAIN 3).
#> Chain 3: 
#> Chain 3: Gradient evaluation took 3e-06 seconds
#> Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.03 seconds.
#> Chain 3: Adjust your expectations accordingly!
#> Chain 3: 
#> Chain 3: 
#> Chain 3: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 3: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 3: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 3: 
#> Chain 3:  Elapsed Time: 0.103 seconds (Warm-up)
#> Chain 3:                0.047 seconds (Sampling)
#> Chain 3:                0.15 seconds (Total)
#> Chain 3: 
#> 
#> SAMPLING FOR MODEL 'eight_schools' NOW (CHAIN 4).
#> Chain 4: 
#> Chain 4: Gradient evaluation took 3e-06 seconds
#> Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.03 seconds.
#> Chain 4: Adjust your expectations accordingly!
#> Chain 4: 
#> Chain 4: 
#> Chain 4: Iteration:    1 / 2000 [  0%]  (Warmup)
#> Chain 4: Iteration:  200 / 2000 [ 10%]  (Warmup)
#> Chain 4: Iteration:  400 / 2000 [ 20%]  (Warmup)
#> Chain 4: Iteration:  600 / 2000 [ 30%]  (Warmup)
#> Chain 4: Iteration:  800 / 2000 [ 40%]  (Warmup)
#> Chain 4: Iteration: 1000 / 2000 [ 50%]  (Warmup)
#> Chain 4: Iteration: 1001 / 2000 [ 50%]  (Sampling)
#> Chain 4: Iteration: 1200 / 2000 [ 60%]  (Sampling)
#> Chain 4: Iteration: 1400 / 2000 [ 70%]  (Sampling)
#> Chain 4: Iteration: 1600 / 2000 [ 80%]  (Sampling)
#> Chain 4: Iteration: 1800 / 2000 [ 90%]  (Sampling)
#> Chain 4: Iteration: 2000 / 2000 [100%]  (Sampling)
#> Chain 4: 
#> Chain 4:  Elapsed Time: 0.079 seconds (Warm-up)
#> Chain 4:                0.046 seconds (Sampling)
#> Chain 4:                0.125 seconds (Total)
#> Chain 4: 
#> Warning: There were 42 divergent transitions after warmup. See
#> https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
#> to find out why this is a problem and how to eliminate them.
#> Warning: Examine the pairs() plot to diagnose sampling problems
#> Warning: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
#> Running the chains for more iterations may help. See
#> https://mc-stan.org/misc/warnings.html#bulk-ess
draws <- as.array(fit, pars = c("mu", "tau", "theta", "lp__"))
np <- nuts_params(fit)
str(np)
#> 'data.frame':	24000 obs. of  4 variables:
#>  $ Chain    : int  1 1 1 1 1 1 1 1 1 1 ...
#>  $ Iteration: int  1 2 3 4 5 6 7 8 9 10 ...
#>  $ Parameter: Factor w/ 6 levels "accept_stat__",..: 1 1 1 1 1 1 1 1 1 1 ...
#>  $ Value    : num  0.974 0.834 0.998 0.992 1 ...
levels(np$Parameter)
#> [1] "accept_stat__" "stepsize__"    "treedepth__"   "n_leapfrog__" 
#> [5] "divergent__"   "energy__"     

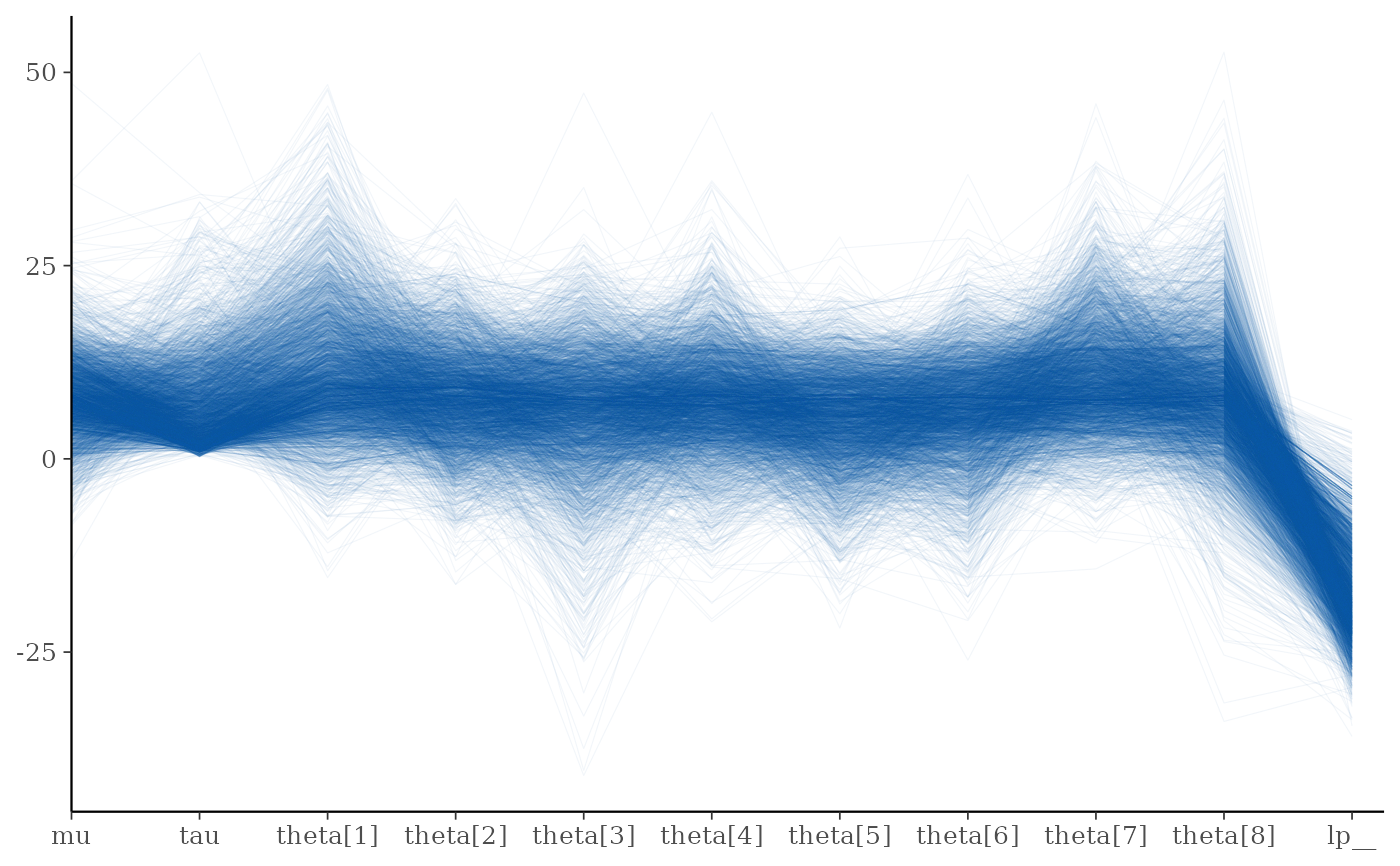
color_scheme_set("brightblue")
mcmc_parcoord(draws, alpha = 0.05)

mcmc_parcoord(draws, np = np)


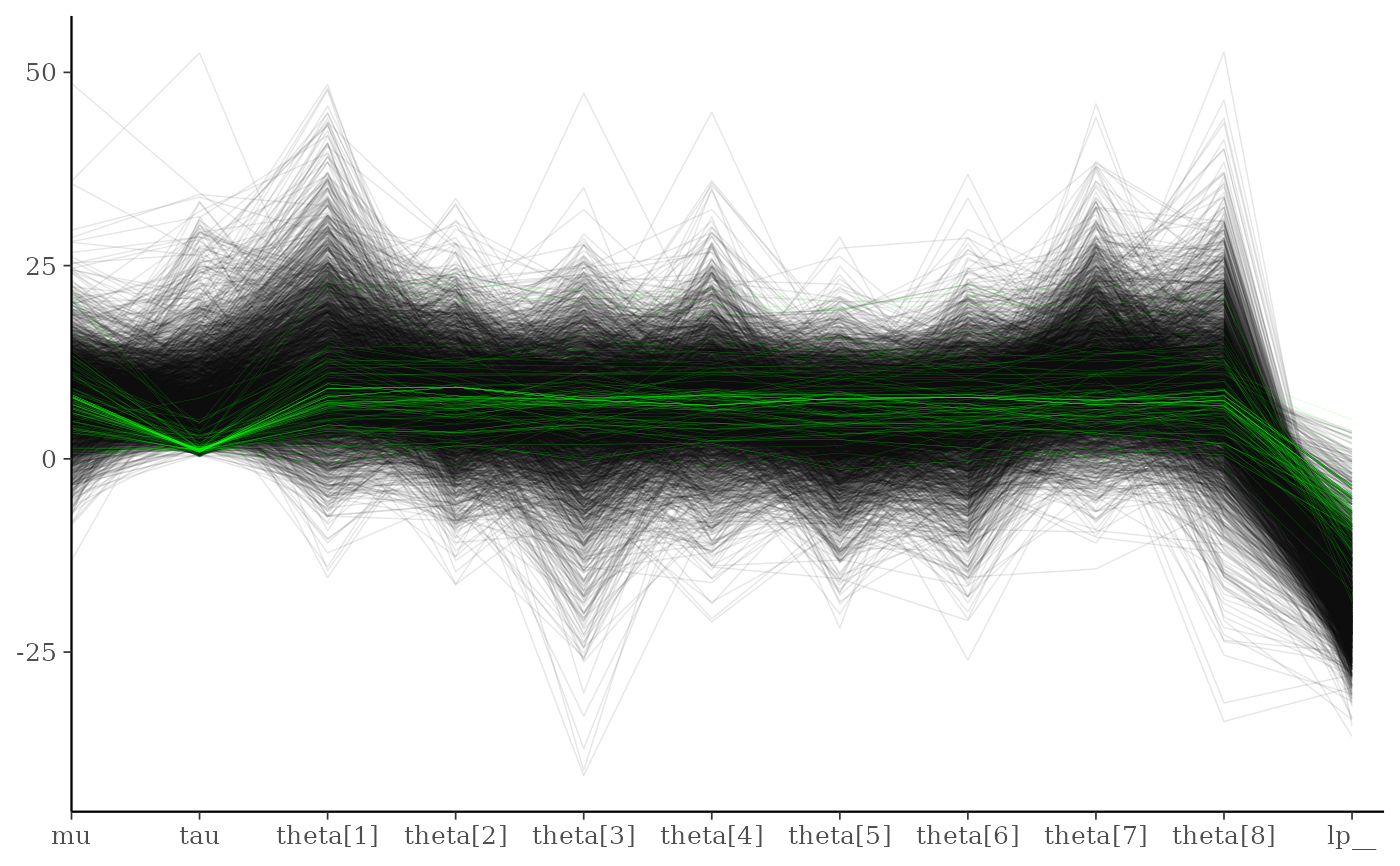
# customize appearance of divergences
color_scheme_set("darkgray")
div_style <- parcoord_style_np(div_color = "green", div_size = 0.05, div_alpha = 0.4)
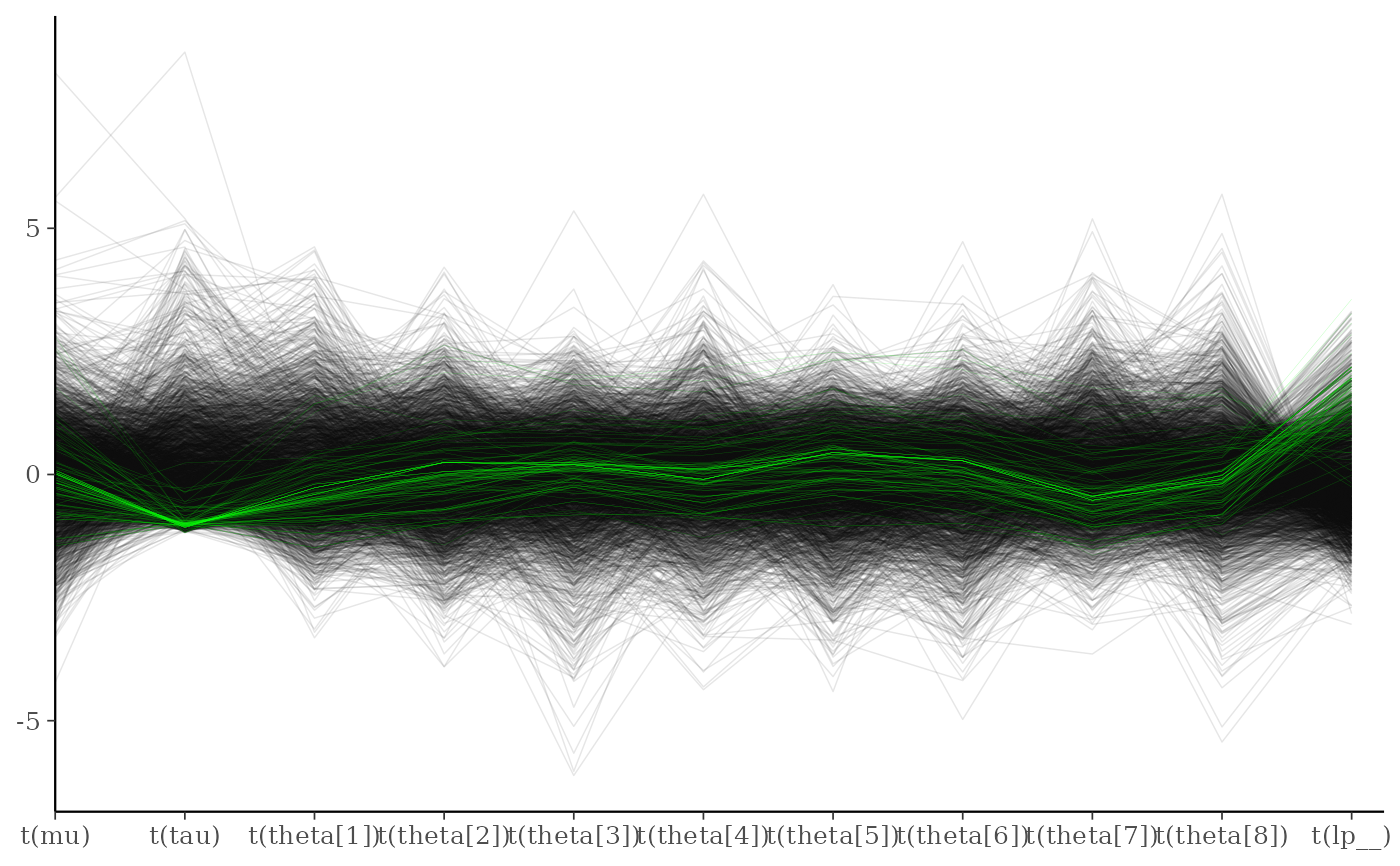
mcmc_parcoord(draws, size = 0.25, alpha = 0.1,
              np = np, np_style = div_style)


# to use a transformation (e.g., standardizing all the variables can be helpful)
# specify the 'transformations' argument (though partial argument name
# matching means we can just use 'trans' or 'transform')
mcmc_parcoord(
  draws,
  transform = function(x) {(x - mean(x)) / sd(x)},
  size = 0.25,
  alpha = 0.1,
  np = np,
  np_style = div_style
 )


# mcmc_parcoord_data returns just the data in a conventient form for plotting
d <- mcmc_parcoord_data(x, np = np)
head(d)
#> # A tibble: 6 × 4
#>    Draw Parameter  Value Divergent
#>   <int> <fct>      <dbl>     <dbl>
#> 1     1 alpha     -14.1          0
#> 2     2 alpha     -20.0          0
#> 3     3 alpha     -21.0          0
#> 4     4 alpha     -36.3          0
#> 5     5 alpha      -7.58         0
#> 6     6 alpha     -10.4          0
tail(d)
#> # A tibble: 6 × 4
#>    Draw Parameter Value Divergent
#>   <int> <fct>     <dbl>     <dbl>
#> 1   995 beta[3]   1.04          0
#> 2   996 beta[3]   1.07          0
#> 3   997 beta[3]   0.983         0
#> 4   998 beta[3]   0.821         0
#> 5   999 beta[3]   0.903         0
#> 6  1000 beta[3]   0.858         0
# }

Arguments

Value

Plot Descriptions

References

See also

Examples