Bayesian nonlinear models with group-specific terms via Stan

Bayesian inference for NLMMs with group-specific coefficients that have unknown covariance matrices with flexible priors.

Usage

stan_nlmer(
  formula,
  data = NULL,
  subset,
  weights,
  na.action,
  offset,
  contrasts = NULL,
  ...,
  prior = normal(autoscale = TRUE),
  prior_aux = exponential(autoscale = TRUE),
  prior_covariance = decov(),
  prior_PD = FALSE,
  algorithm = c("sampling", "meanfield", "fullrank"),
  adapt_delta = NULL,
  QR = FALSE,
  sparse = FALSE
)

Arguments

formula, data

Same as for nlmer. We strongly advise against omitting the data argument. Unless data is specified (and is a data frame) many post-estimation functions (including update, loo, kfold) are not guaranteed to work properly.

subset, weights, offset

Same as glm.

na.action, contrasts

Same as glm, but rarely specified.

...

Further arguments passed to the function in the rstan package (sampling, vb, or optimizing), corresponding to the estimation method named by algorithm. For example, if algorithm is "sampling" it is possible to specify iter, chains, cores, and other MCMC controls.

Another useful argument that can be passed to rstan via ... is refresh, which specifies how often to print updates when sampling (i.e., show the progress every refresh iterations). refresh=0 turns off the iteration updates.

prior

The prior distribution for the (non-hierarchical) regression coefficients.

The default priors are described in the vignette Prior Distributions for rstanarm Models. If not using the default, prior should be a call to one of the various functions provided by rstanarm for specifying priors. The subset of these functions that can be used for the prior on the coefficients can be grouped into several "families":

Family	Functions
Student t family	`normal`, `student_t`, `cauchy`
Hierarchical shrinkage family	`hs`, `hs_plus`
Laplace family	`laplace`, `lasso`
Product normal family	`product_normal`

See the priors help page for details on the families and how to specify the arguments for all of the functions in the table above. To omit a prior —i.e., to use a flat (improper) uniform prior— prior can be set to NULL, although this is rarely a good idea.

Note: Unless QR=TRUE, if prior is from the Student t family or Laplace family, and if the autoscale argument to the function used to specify the prior (e.g. normal) is left at its default and recommended value of TRUE, then the default or user-specified prior scale(s) may be adjusted internally based on the scales of the predictors. See the priors help page and the Prior Distributions vignette for details on the rescaling and the prior_summary function for a summary of the priors used for a particular model.

prior_aux

The prior distribution for the "auxiliary" parameter (if applicable). The "auxiliary" parameter refers to a different parameter depending on the family. For Gaussian models prior_aux controls "sigma", the error standard deviation. For negative binomial models prior_aux controls "reciprocal_dispersion", which is similar to the "size" parameter of rnbinom: smaller values of "reciprocal_dispersion" correspond to greater dispersion. For gamma models prior_aux sets the prior on to the "shape" parameter (see e.g., rgamma), and for inverse-Gaussian models it is the so-called "lambda" parameter (which is essentially the reciprocal of a scale parameter). Binomial and Poisson models do not have auxiliary parameters.

The default prior is described in the vignette Prior Distributions for rstanarm Models. If not using the default, prior_aux can be a call to exponential to use an exponential distribution, or normal, student_t or cauchy, which results in a half-normal, half-t, or half-Cauchy prior. See priors for details on these functions. To omit a prior —i.e., to use a flat (improper) uniform prior— set prior_aux to NULL.

prior_covariance

Cannot be NULL; see decov for more information about the default arguments.

prior_PD

A logical scalar (defaulting to FALSE) indicating whether to draw from the prior predictive distribution instead of conditioning on the outcome.

algorithm

A string (possibly abbreviated) indicating the estimation approach to use. Can be "sampling" for MCMC (the default), "optimizing" for optimization, "meanfield" for variational inference with independent normal distributions, or "fullrank" for variational inference with a multivariate normal distribution. See rstanarm-package for more details on the estimation algorithms. NOTE: not all fitting functions support all four algorithms.

adapt_delta

Only relevant if algorithm="sampling". See the adapt_delta help page for details.

QR

A logical scalar defaulting to FALSE, but if TRUE applies a scaled qr decomposition to the design matrix. The transformation does not change the likelihood of the data but is recommended for computational reasons when there are multiple predictors. See the QR-argument documentation page for details on how rstanarm does the transformation and important information about how to interpret the prior distributions of the model parameters when using QR=TRUE.

sparse

A logical scalar (defaulting to FALSE) indicating whether to use a sparse representation of the design (X) matrix. If TRUE, the the design matrix is not centered (since that would destroy the sparsity) and likewise it is not possible to specify both QR = TRUE and sparse = TRUE. Depending on how many zeros there are in the design matrix, setting sparse = TRUE may make the code run faster and can consume much less RAM.

Value

A stanreg object is returned for stan_nlmer.

Details

The stan_nlmer function is similar in syntax to nlmer but rather than performing (approximate) maximum marginal likelihood estimation, Bayesian estimation is by default performed via MCMC. The Bayesian model adds independent priors on the "coefficients" — which are really intercepts — in the same way as stan_nlmer and priors on the terms of a decomposition of the covariance matrices of the group-specific parameters. See priors for more information about the priors.

The supported transformation functions are limited to the named "self-starting" functions in the stats library: SSasymp, SSasympOff, SSasympOrig, SSbiexp, SSfol, SSfpl, SSgompertz, SSlogis, SSmicmen, and SSweibull.

Examples

if (.Platform$OS.type != "windows" || .Platform$r_arch !="i386") {
# \donttest{
data("Orange", package = "datasets")
Orange$circumference <- Orange$circumference / 100
Orange$age <- Orange$age / 100
fit <- stan_nlmer(
  circumference ~ SSlogis(age, Asym, xmid, scal) ~ Asym|Tree, 
  data = Orange, 
  # for speed only
  chains = 1, 
  iter = 1000
 ) 
print(fit)
posterior_interval(fit)
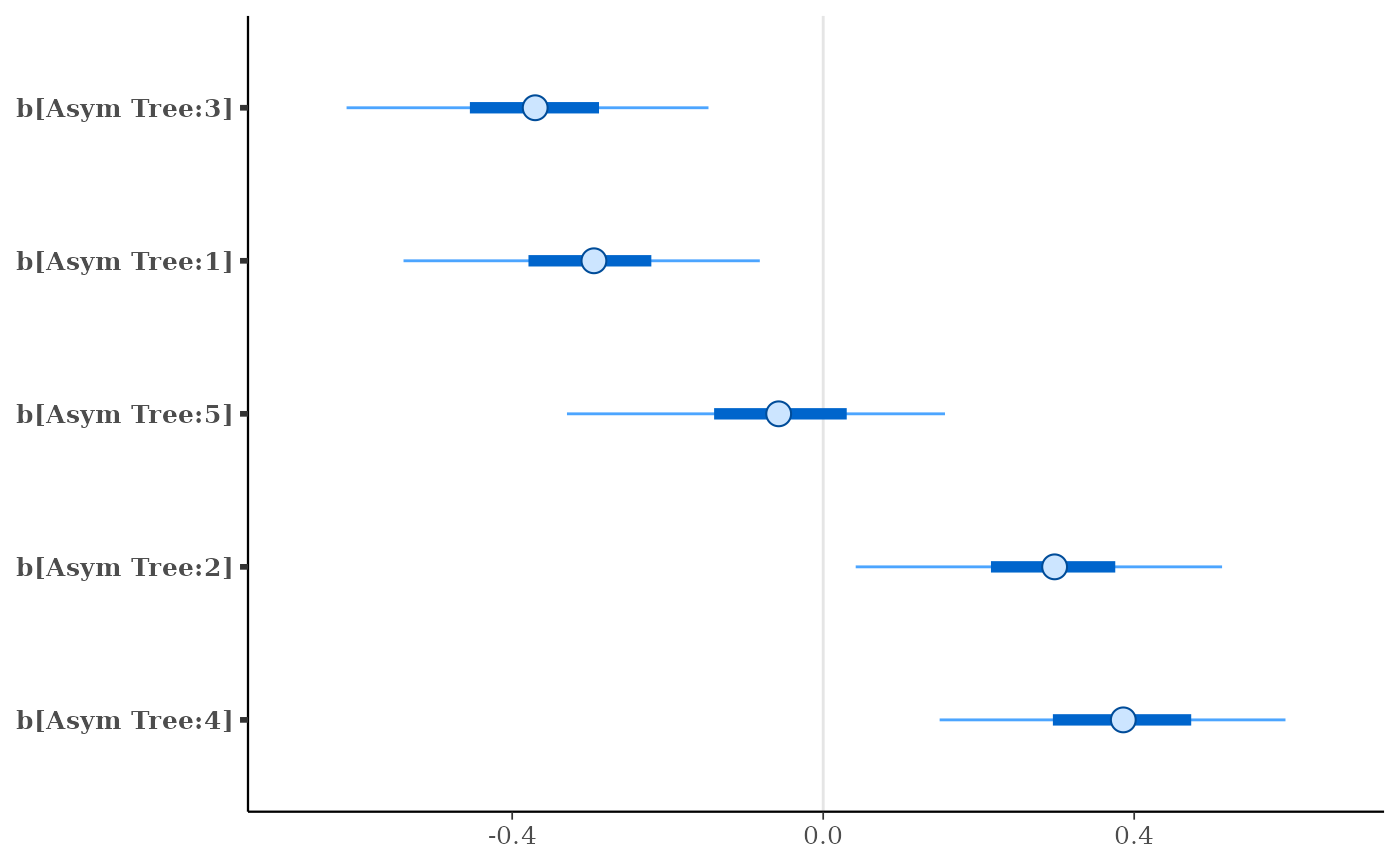
plot(fit, regex_pars = "b\\[")
# }
}
#> Warning: number of iterations exceeded maximum of 0
#> 
#> SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
#> Chain 1: 
#> Chain 1: Gradient evaluation took 3.9e-05 seconds
#> Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.39 seconds.
#> Chain 1: Adjust your expectations accordingly!
#> Chain 1: 
#> Chain 1: 
#> Chain 1: Iteration:   1 / 1000 [  0%]  (Warmup)
#> Chain 1: Iteration: 100 / 1000 [ 10%]  (Warmup)
#> Chain 1: Iteration: 200 / 1000 [ 20%]  (Warmup)
#> Chain 1: Iteration: 300 / 1000 [ 30%]  (Warmup)
#> Chain 1: Iteration: 400 / 1000 [ 40%]  (Warmup)
#> Chain 1: Iteration: 500 / 1000 [ 50%]  (Warmup)
#> Chain 1: Iteration: 501 / 1000 [ 50%]  (Sampling)
#> Chain 1: Iteration: 600 / 1000 [ 60%]  (Sampling)
#> Chain 1: Iteration: 700 / 1000 [ 70%]  (Sampling)
#> Chain 1: Iteration: 800 / 1000 [ 80%]  (Sampling)
#> Chain 1: Iteration: 900 / 1000 [ 90%]  (Sampling)
#> Chain 1: Iteration: 1000 / 1000 [100%]  (Sampling)
#> Chain 1: 
#> Chain 1:  Elapsed Time: 0.771 seconds (Warm-up)
#> Chain 1:                0.387 seconds (Sampling)
#> Chain 1:                1.158 seconds (Total)
#> Chain 1: 
#> stan_nlmer
#>  family:       gaussian [inv_SSlogis]
#>  formula:      circumference ~ SSlogis(age, Asym, xmid, scal) ~ Asym | Tree
#>  observations: 35
#> ------
#>      Median MAD_SD
#> Asym 1.9    0.1   
#> xmid 7.2    0.3   
#> scal 3.4    0.3   
#> 
#> Auxiliary parameter(s):
#>       Median MAD_SD
#> sigma 0.1    0.0   
#> 
#> Error terms:
#>  Groups   Name Std.Dev.
#>  Tree     Asym 0.313   
#>  Residual      0.089   
#> Num. levels: Tree 5 
#> 
#> ------
#> * For help interpreting the printed output see ?print.stanreg
#> * For info on the priors used see ?prior_summary.stanreg