Bayesian generalized linear additive models with optional group-specific terms via Stan

Bayesian inference for GAMMs with flexible priors.

stan_gamm4(
  formula,
  random = NULL,
  family = gaussian(),
  data,
  weights = NULL,
  subset = NULL,
  na.action,
  knots = NULL,
  drop.unused.levels = TRUE,
  ...,
  prior = default_prior_coef(family),
  prior_intercept = default_prior_intercept(family),
  prior_smooth = exponential(autoscale = FALSE),
  prior_aux = exponential(autoscale = TRUE),
  prior_covariance = decov(),
  prior_PD = FALSE,
  algorithm = c("sampling", "meanfield", "fullrank"),
  adapt_delta = NULL,
  QR = FALSE,
  sparse = FALSE
)

plot_nonlinear(
  x,
  smooths,
  ...,
  prob = 0.9,
  facet_args = list(),
  alpha = 1,
  size = 0.75
)

Arguments

formula, random, family, data, knots, drop.unused.levels

Same as for gamm4. We strongly advise against omitting the data argument. Unless data is specified (and is a data frame) many post-estimation functions (including update, loo, kfold) are not guaranteed to work properly.

subset, weights, na.action

Same as glm, but rarely specified.

...

Further arguments passed to sampling (e.g. iter, chains, cores, etc.) or to vb (if algorithm is "meanfield" or "fullrank").

prior

The prior distribution for the (non-hierarchical) regression coefficients.

The default priors are described in the vignette Prior Distributions for rstanarm Models. If not using the default, prior should be a call to one of the various functions provided by rstanarm for specifying priors. The subset of these functions that can be used for the prior on the coefficients can be grouped into several "families":

Family	Functions
Student t family	`normal`, `student_t`, `cauchy`
Hierarchical shrinkage family	`hs`, `hs_plus`
Laplace family	`laplace`, `lasso`
Product normal family	`product_normal`

See the priors help page for details on the families and how to specify the arguments for all of the functions in the table above. To omit a prior ---i.e., to use a flat (improper) uniform prior--- prior can be set to NULL, although this is rarely a good idea.

Note: Unless QR=TRUE, if prior is from the Student t family or Laplace family, and if the autoscale argument to the function used to specify the prior (e.g. normal) is left at its default and recommended value of TRUE, then the default or user-specified prior scale(s) may be adjusted internally based on the scales of the predictors. See the priors help page and the Prior Distributions vignette for details on the rescaling and the prior_summary function for a summary of the priors used for a particular model.

prior_intercept

The prior distribution for the intercept (after centering all predictors, see note below).

The default prior is described in the vignette Prior Distributions for rstanarm Models. If not using the default, prior_intercept can be a call to normal, student_t or cauchy. See the priors help page for details on these functions. To omit a prior on the intercept ---i.e., to use a flat (improper) uniform prior--- prior_intercept can be set to NULL.

Note: If using a dense representation of the design matrix ---i.e., if the sparse argument is left at its default value of FALSE--- then the prior distribution for the intercept is set so it applies to the value when all predictors are centered (you don't need to manually center them). This is explained further in [Prior Distributions for rstanarm Models](https://mc-stan.org/rstanarm/articles/priors.html) If you prefer to specify a prior on the intercept without the predictors being auto-centered, then you have to omit the intercept from the formula and include a column of ones as a predictor, in which case some element of prior specifies the prior on it, rather than prior_intercept. Regardless of how prior_intercept is specified, the reported estimates of the intercept always correspond to a parameterization without centered predictors (i.e., same as in glm).

prior_smooth

The prior distribution for the hyperparameters in GAMs, with lower values yielding less flexible smooth functions.

prior_smooth can be a call to exponential to use an exponential distribution, or normal, student_t or cauchy, which results in a half-normal, half-t, or half-Cauchy prior. See priors for details on these functions. To omit a prior ---i.e., to use a flat (improper) uniform prior--- set prior_smooth to NULL. The number of hyperparameters depends on the model specification but a scalar prior will be recylced as necessary to the appropriate length.

prior_aux

The prior distribution for the "auxiliary" parameter (if applicable). The "auxiliary" parameter refers to a different parameter depending on the family. For Gaussian models prior_aux controls "sigma", the error standard deviation. For negative binomial models prior_aux controls "reciprocal_dispersion", which is similar to the "size" parameter of rnbinom: smaller values of "reciprocal_dispersion" correspond to greater dispersion. For gamma models prior_aux sets the prior on to the "shape" parameter (see e.g., rgamma), and for inverse-Gaussian models it is the so-called "lambda" parameter (which is essentially the reciprocal of a scale parameter). Binomial and Poisson models do not have auxiliary parameters.

The default prior is described in the vignette Prior Distributions for rstanarm Models. If not using the default, prior_aux can be a call to exponential to use an exponential distribution, or normal, student_t or cauchy, which results in a half-normal, half-t, or half-Cauchy prior. See priors for details on these functions. To omit a prior ---i.e., to use a flat (improper) uniform prior--- set prior_aux to NULL.

prior_covariance

Cannot be NULL; see decov for more information about the default arguments.

prior_PD

A logical scalar (defaulting to FALSE) indicating whether to draw from the prior predictive distribution instead of conditioning on the outcome.

algorithm

A string (possibly abbreviated) indicating the estimation approach to use. Can be "sampling" for MCMC (the default), "optimizing" for optimization, "meanfield" for variational inference with independent normal distributions, or "fullrank" for variational inference with a multivariate normal distribution. See rstanarm-package for more details on the estimation algorithms. NOTE: not all fitting functions support all four algorithms.

adapt_delta

Only relevant if algorithm="sampling". See the adapt_delta help page for details.

A logical scalar defaulting to FALSE, but if TRUE applies a scaled qr decomposition to the design matrix. The transformation does not change the likelihood of the data but is recommended for computational reasons when there are multiple predictors. See the QR-argument documentation page for details on how rstanarm does the transformation and important information about how to interpret the prior distributions of the model parameters when using QR=TRUE.

sparse

A logical scalar (defaulting to FALSE) indicating whether to use a sparse representation of the design (X) matrix. If TRUE, the the design matrix is not centered (since that would destroy the sparsity) and likewise it is not possible to specify both QR = TRUE and sparse = TRUE. Depending on how many zeros there are in the design matrix, setting sparse = TRUE may make the code run faster and can consume much less RAM.

An object produced by stan_gamm4.

smooths

An optional character vector specifying a subset of the smooth functions specified in the call to stan_gamm4. The default is include all smooth terms.

prob

For univarite smooths, a scalar between 0 and 1 governing the width of the uncertainty interval.

facet_args

An optional named list of arguments passed to facet_wrap (other than the facets argument).

alpha, size

For univariate smooths, passed to geom_ribbon. For bivariate smooths, size/2 is passed to geom_contour.

Value

A stanreg object is returned for stan_gamm4.

plot_nonlinear returns a ggplot object.

Details

The stan_gamm4 function is similar in syntax to gamm4 in the gamm4 package. But rather than performing (restricted) maximum likelihood estimation with the lme4 package, the stan_gamm4 function utilizes MCMC to perform Bayesian estimation. The Bayesian model adds priors on the common regression coefficients (in the same way as stan_glm), priors on the standard deviations of the smooth terms, and a prior on the decomposition of the covariance matrices of any group-specific parameters (as in stan_glmer). Estimating these models via MCMC avoids the optimization issues that often crop up with GAMMs and provides better estimates for the uncertainty in the parameter estimates.

See gamm4 for more information about the model specicification and priors for more information about the priors on the main coefficients. The formula should include at least one smooth term, which can be specified in any way that is supported by the jagam function in the mgcv package. The prior_smooth argument should be used to specify a prior on the unknown standard deviations that govern how smooth the smooth function is. The prior_covariance argument can be used to specify the prior on the components of the covariance matrix for any (optional) group-specific terms. The gamm4 function in the gamm4 package uses group-specific terms to implement the departure from linearity in the smooth terms, but that is not the case for stan_gamm4 where the group-specific terms are exactly the same as in stan_glmer.

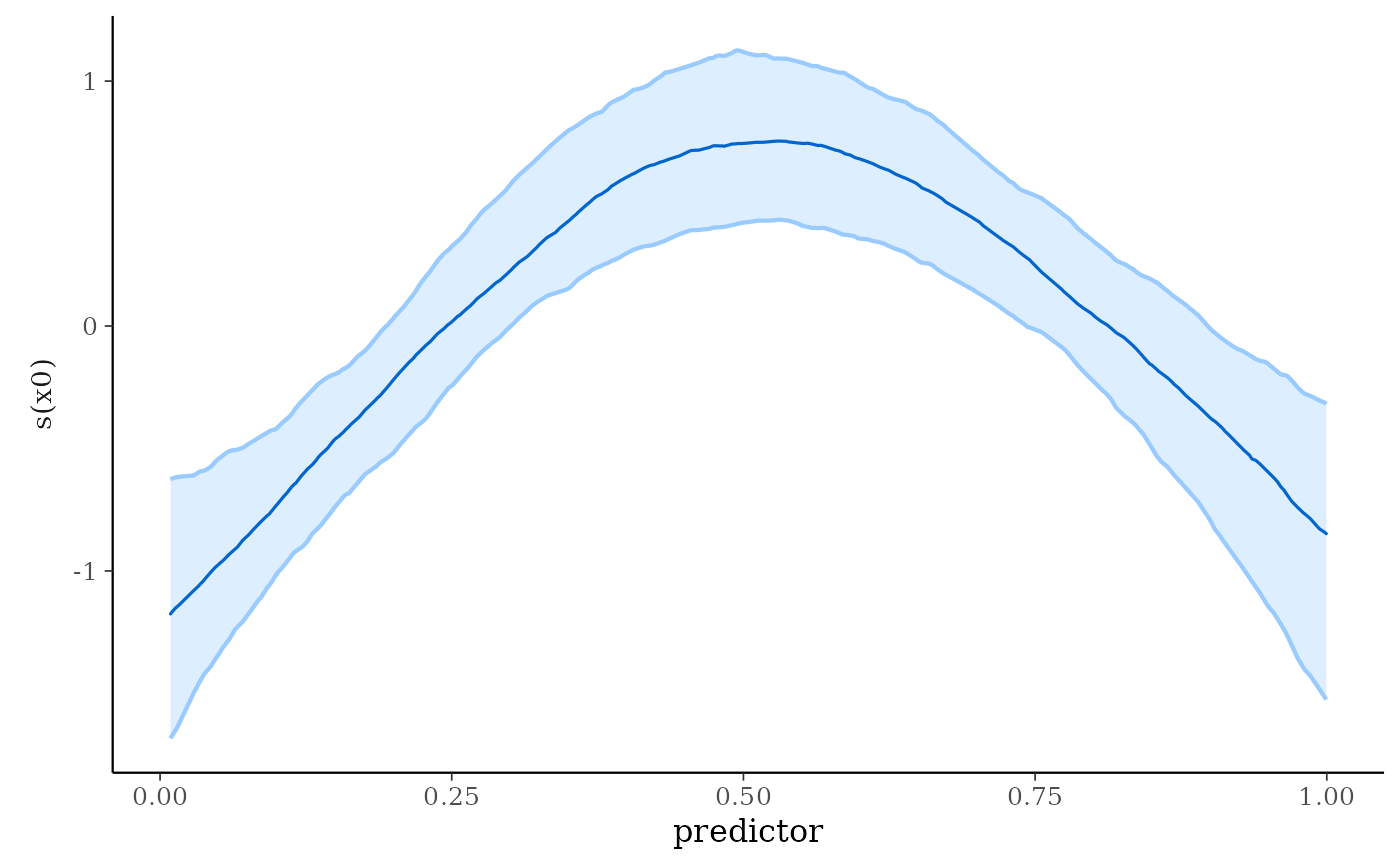
The plot_nonlinear function creates a ggplot object with one facet for each smooth function specified in the call to stan_gamm4 in the case where all smooths are univariate. A subset of the smooth functions can be specified using the smooths argument, which is necessary to plot a bivariate smooth or to exclude the bivariate smooth and plot the univariate ones. In the bivariate case, a plot is produced using geom_contour. In the univariate case, the resulting plot is conceptually similar to plot.gam except the outer lines here demark the edges of posterior uncertainty intervals (credible intervals) rather than confidence intervals and the inner line is the posterior median of the function rather than the function implied by a point estimate. To change the colors used in the plot see color_scheme_set.

References

Crainiceanu, C., Ruppert D., and Wand, M. (2005). Bayesian analysis for penalized spline regression using WinBUGS. Journal of Statistical Software. 14(14), 1--22. https://www.jstatsoft.org/article/view/v014i14

Examples

# from example(gamm4, package = "gamm4"), prefixing gamm4() call with stan_
# \donttest{
dat <- mgcv::gamSim(1, n = 400, scale = 2) ## simulate 4 term additive truth
#> Gu & Wahba 4 term additive model
## Now add 20 level random effect `fac'...
dat$fac <- fac <- as.factor(sample(1:20, 400, replace = TRUE))
dat$y <- dat$y + model.matrix(~ fac - 1) %*% rnorm(20) * .5

br <- stan_gamm4(y ~ s(x0) + x1 + s(x2), data = dat, random = ~ (1 | fac),
                 chains = 1, iter = 500) # for example speed
#> 
#> SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
#> Chain 1: 
#> Chain 1: Gradient evaluation took 9.8e-05 seconds
#> Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.98 seconds.
#> Chain 1: Adjust your expectations accordingly!
#> Chain 1: 
#> Chain 1: 
#> Chain 1: Iteration:   1 / 500 [  0%]  (Warmup)
#> Chain 1: Iteration:  50 / 500 [ 10%]  (Warmup)
#> Chain 1: Iteration: 100 / 500 [ 20%]  (Warmup)
#> Chain 1: Iteration: 150 / 500 [ 30%]  (Warmup)
#> Chain 1: Iteration: 200 / 500 [ 40%]  (Warmup)
#> Chain 1: Iteration: 250 / 500 [ 50%]  (Warmup)
#> Chain 1: Iteration: 251 / 500 [ 50%]  (Sampling)
#> Chain 1: Iteration: 300 / 500 [ 60%]  (Sampling)
#> Chain 1: Iteration: 350 / 500 [ 70%]  (Sampling)
#> Chain 1: Iteration: 400 / 500 [ 80%]  (Sampling)
#> Chain 1: Iteration: 450 / 500 [ 90%]  (Sampling)
#> Chain 1: Iteration: 500 / 500 [100%]  (Sampling)
#> Chain 1: 
#> Chain 1:  Elapsed Time: 3.96087 seconds (Warm-up)
#> Chain 1:                1.7028 seconds (Sampling)
#> Chain 1:                5.66367 seconds (Total)
#> Chain 1: 
#> Warning: There were 8 divergent transitions after warmup. Increasing adapt_delta above 0.95 may help. See
#> http://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
#> Warning: Examine the pairs() plot to diagnose sampling problems
#> Warning: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
#> Running the chains for more iterations may help. See
#> http://mc-stan.org/misc/warnings.html#bulk-ess
#> Warning: Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
#> Running the chains for more iterations may help. See
#> http://mc-stan.org/misc/warnings.html#tail-ess
print(br)
#> stan_gamm4
#>  family:       gaussian [identity]
#>  formula:      y ~ s(x0) + x1 + s(x2)
#>  observations: 400
#> ------
#>             Median MAD_SD
#> (Intercept)   4.3    0.2 
#> x1            6.4    0.4 
#> s(x0).1       0.9    2.2 
#> s(x0).2       0.5    1.9 
#> s(x0).3       0.5    2.2 
#> s(x0).4       0.6    1.8 
#> s(x0).5       1.3    1.9 
#> s(x0).6      -1.9    1.2 
#> s(x0).7      -0.7    0.8 
#> s(x0).8      -2.7    1.6 
#> s(x0).9      -0.1    1.1 
#> s(x2).1     -42.9   12.0 
#> s(x2).2      -5.7    8.1 
#> s(x2).3      39.5    8.8 
#> s(x2).4     -40.3    6.1 
#> s(x2).5       4.2    4.5 
#> s(x2).6     -10.4    2.0 
#> s(x2).7       8.9    1.6 
#> s(x2).8      -9.8    5.1 
#> s(x2).9       3.5    5.4 
#> 
#> Auxiliary parameter(s):
#>       Median MAD_SD
#> sigma 2.0    0.1   
#> 
#> Smoothing terms:
#>                   Median MAD_SD
#> smooth_sd[s(x0)1]  2.3    0.8  
#> smooth_sd[s(x0)2]  1.5    1.4  
#> smooth_sd[s(x2)1] 18.6    2.9  
#> smooth_sd[s(x2)2]  3.6    3.8  
#> 
#> Error terms:
#>  Groups   Name        Std.Dev.
#>  fac      (Intercept) 0.45    
#>  Residual             2.02    
#> Num. levels: fac 20 
#> 
#> ------
#> * For help interpreting the printed output see ?print.stanreg
#> * For info on the priors used see ?prior_summary.stanreg
plot_nonlinear(br)
plot_nonlinear(br, smooths = "s(x0)", alpha = 2/3)
# }