Compare MCMC estimates to "true" parameter values

Plots comparing MCMC estimates to "true" parameter values. Before fitting a model to real data it is useful to simulate data according to the model using known (fixed) parameter values and to check that these "true" parameter values are (approximately) recovered by fitting the model to the simulated data. See the Plot Descriptions section, below, for details on the available plots.

mcmc_recover_intervals(
  x,
  true,
  batch = rep(1, length(true)),
  ...,
  facet_args = list(),
  prob = 0.5,
  prob_outer = 0.9,
  point_est = c("median", "mean", "none"),
  size = 4,
  alpha = 1
)

mcmc_recover_scatter(
  x,
  true,
  batch = rep(1, length(true)),
  ...,
  facet_args = list(),
  point_est = c("median", "mean"),
  size = 3,
  alpha = 1
)

mcmc_recover_hist(
  x,
  true,
  ...,
  facet_args = list(),
  binwidth = NULL,
  bins = NULL,
  breaks = NULL
)

Arguments

x

An object containing MCMC draws:

A 3-D array, matrix, list of matrices, or data frame. The MCMC-overview page provides details on how to specify each these.
A draws object from the posterior package (e.g., draws_array, draws_rvars, etc.).
An object with an as.array() method that returns the same kind of 3-D array described on the MCMC-overview page.

true

A numeric vector of "true" values of the parameters in x. There should be one value in true for each parameter included in x and the order of the parameters in true should be the same as the order of the parameters in x.

batch

Optionally, a vector-like object (numeric, character, integer, factor) used to split the parameters into batches. If batch is specified, it must have the same length as true and be in the same order as true. Parameters in the same batch will be grouped together in the same facet in the plot (see the Examples section, below). The default is to group all parameters together into a single batch. Changing the default is most useful when parameters are on very different scales, in which case batch can be used to group them into batches within which it makes sense to use the same y-axis.

...

Currently unused.

facet_args

A named list of arguments (other than facets) passed to ggplot2::facet_wrap() or ggplot2::facet_grid() to control faceting. Note: if scales is not included in facet_args then bayesplot may use scales="free" as the default (depending on the plot) instead of the ggplot2 default of scales="fixed".

prob

The probability mass to include in the inner interval. The default is 0.5 (50% interval).

prob_outer

The probability mass to include in the outer interval. The default is 0.9 (90% interval).

point_est

The point estimate to show. Either "median" (the default), "mean", or "none".

size, alpha

Passed to ggplot2::geom_point() to control the appearance of plotted points.

binwidth

Passed to ggplot2::geom_histogram() to override the default binwidth.

bins

Passed to ggplot2::geom_histogram() to override the default binwidth.

breaks

Passed to ggplot2::geom_histogram() as an alternative to binwidth.

Value

A ggplot object that can be further customized using the ggplot2 package.

Plot Descriptions

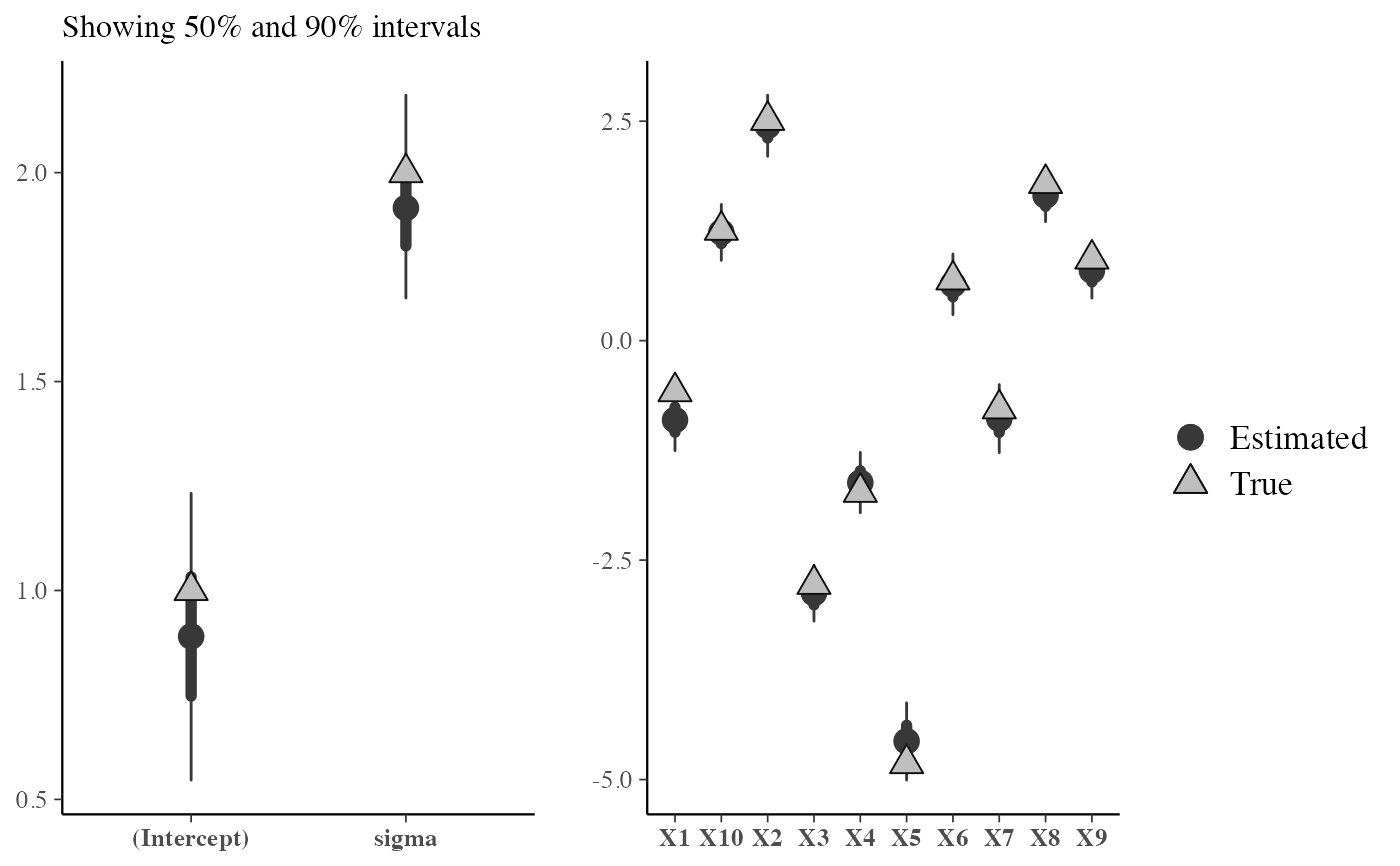
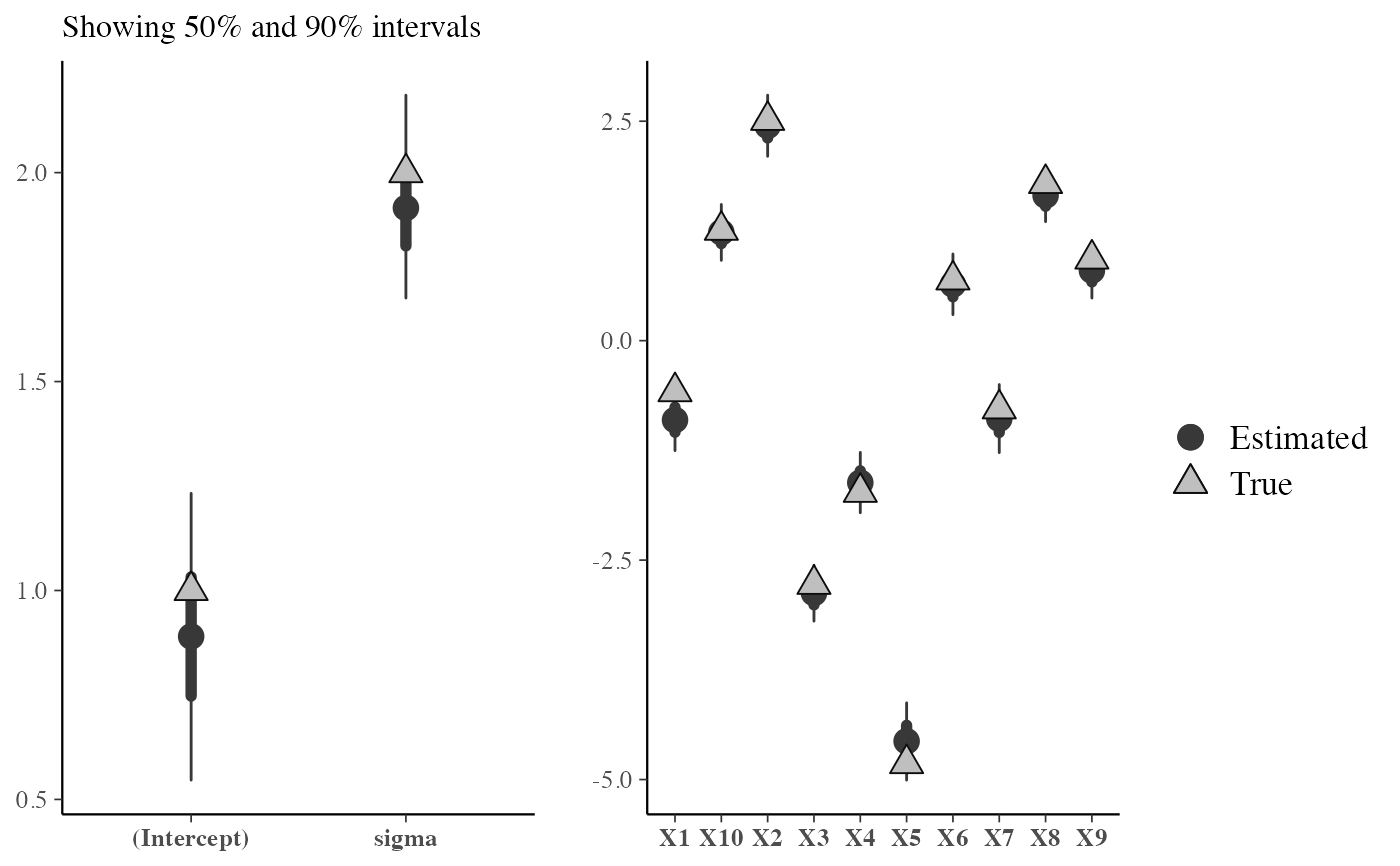
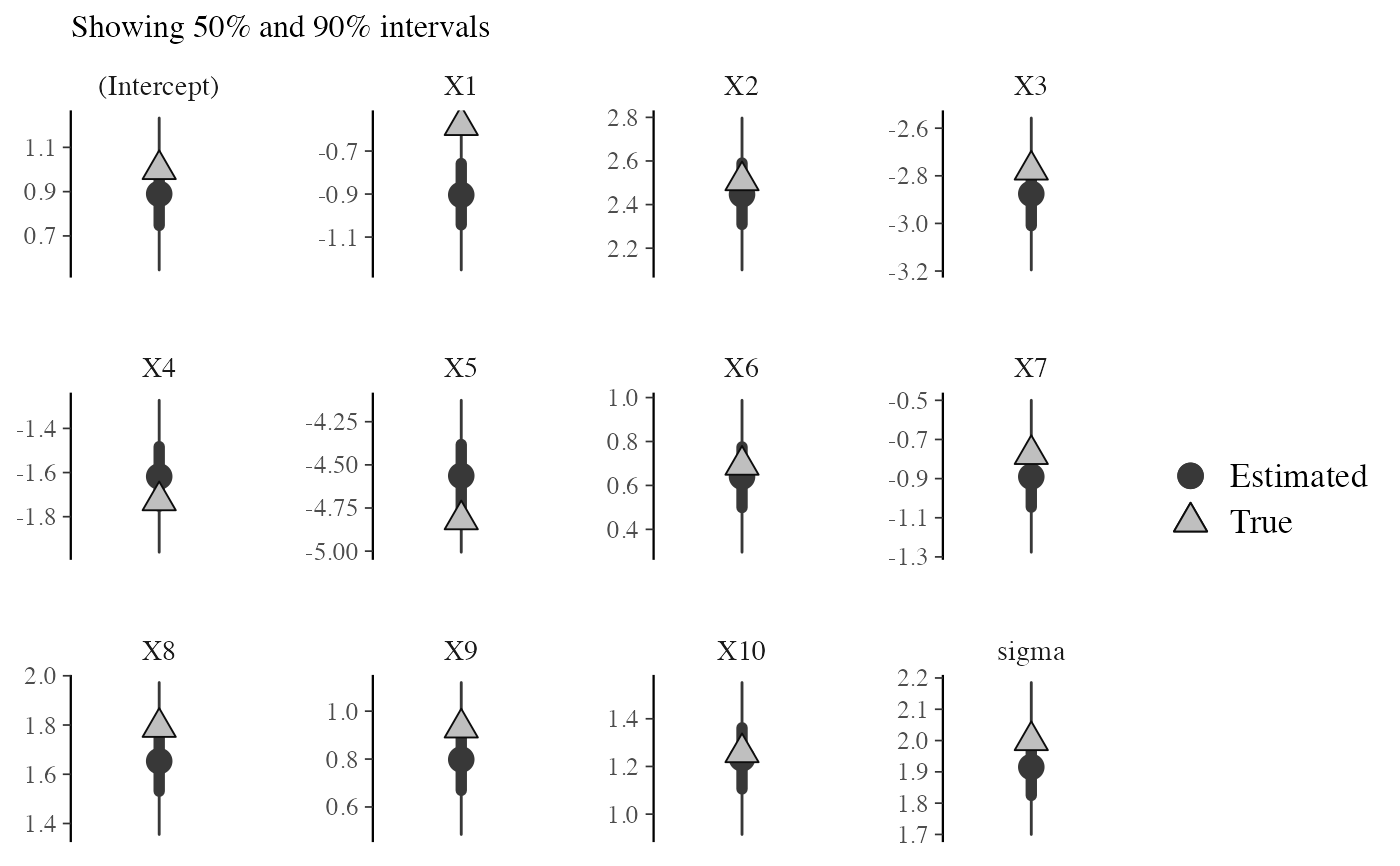
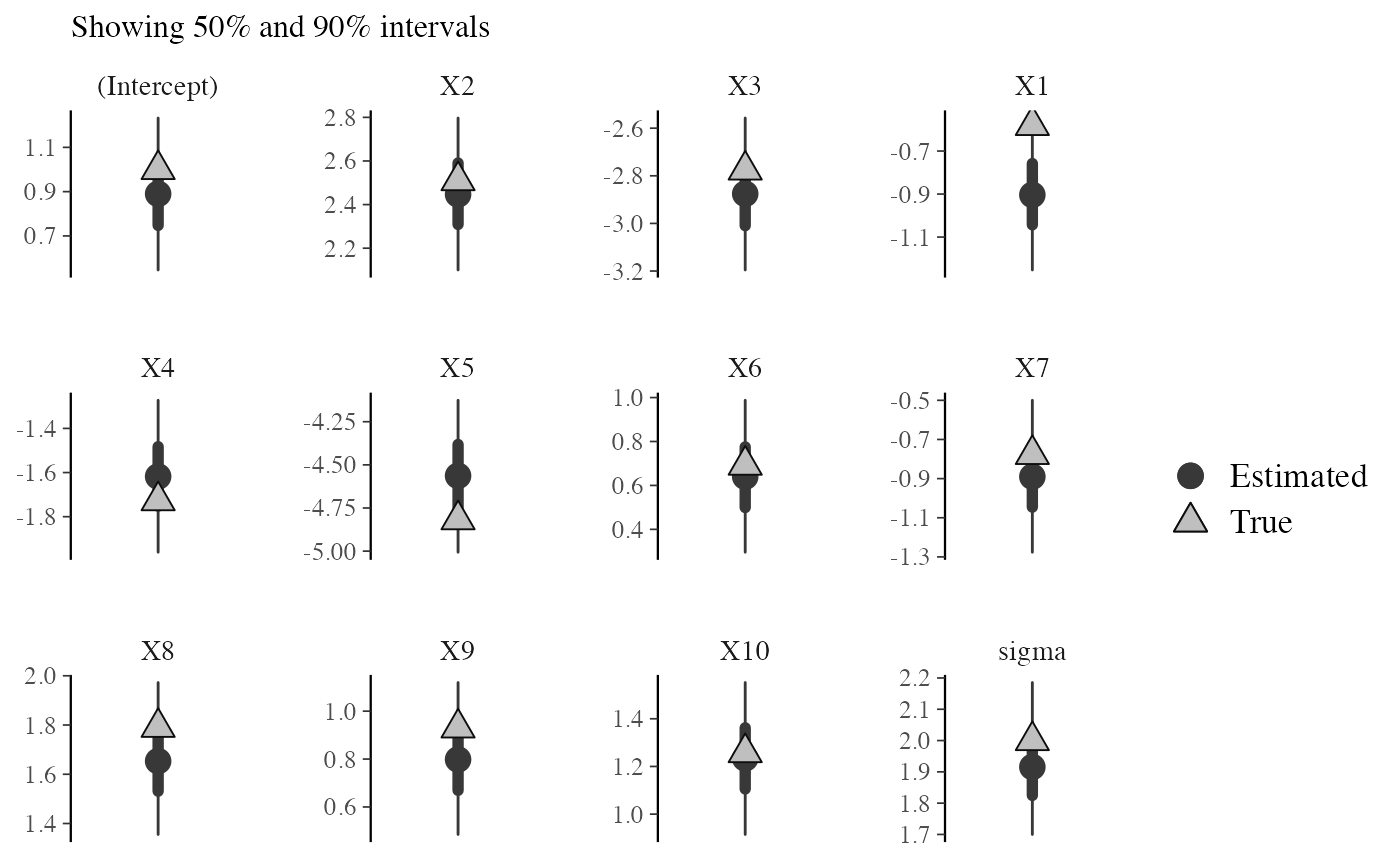
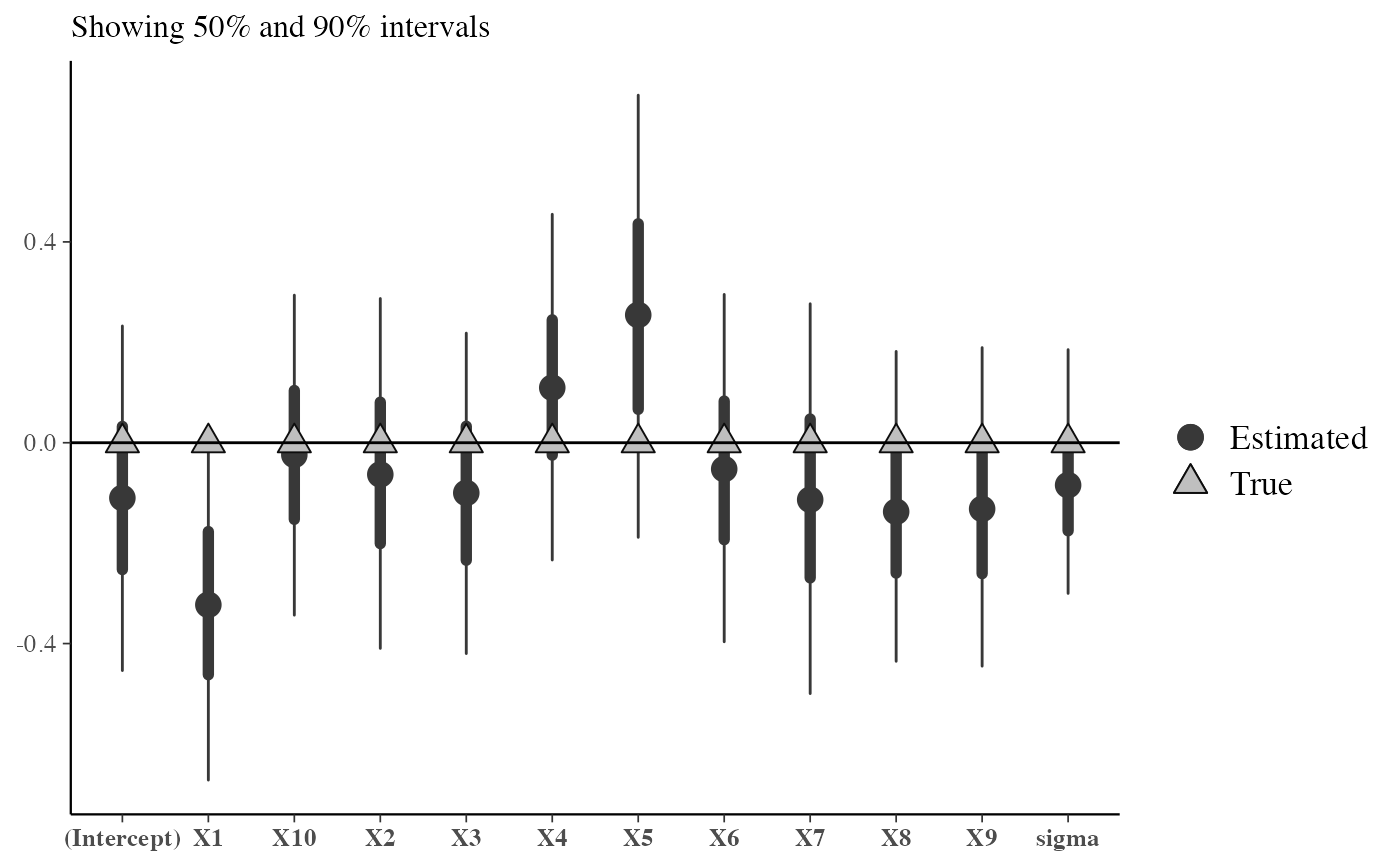
mcmc_recover_intervals(): Central intervals and point estimates computed from MCMC draws, with "true" values plotted using a different shape.
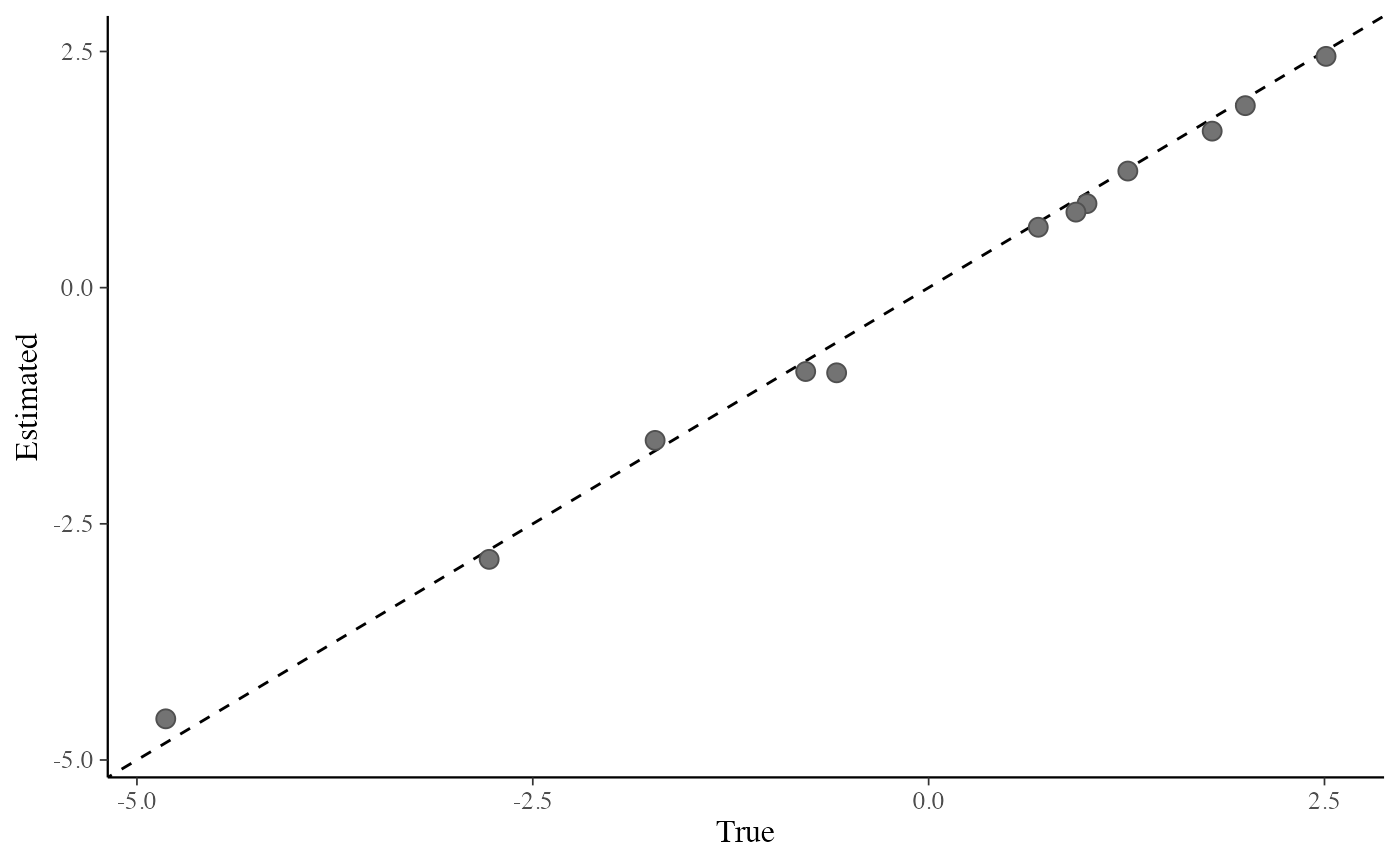
mcmc_recover_scatter(): Scatterplot of posterior means (or medians) against "true" values.
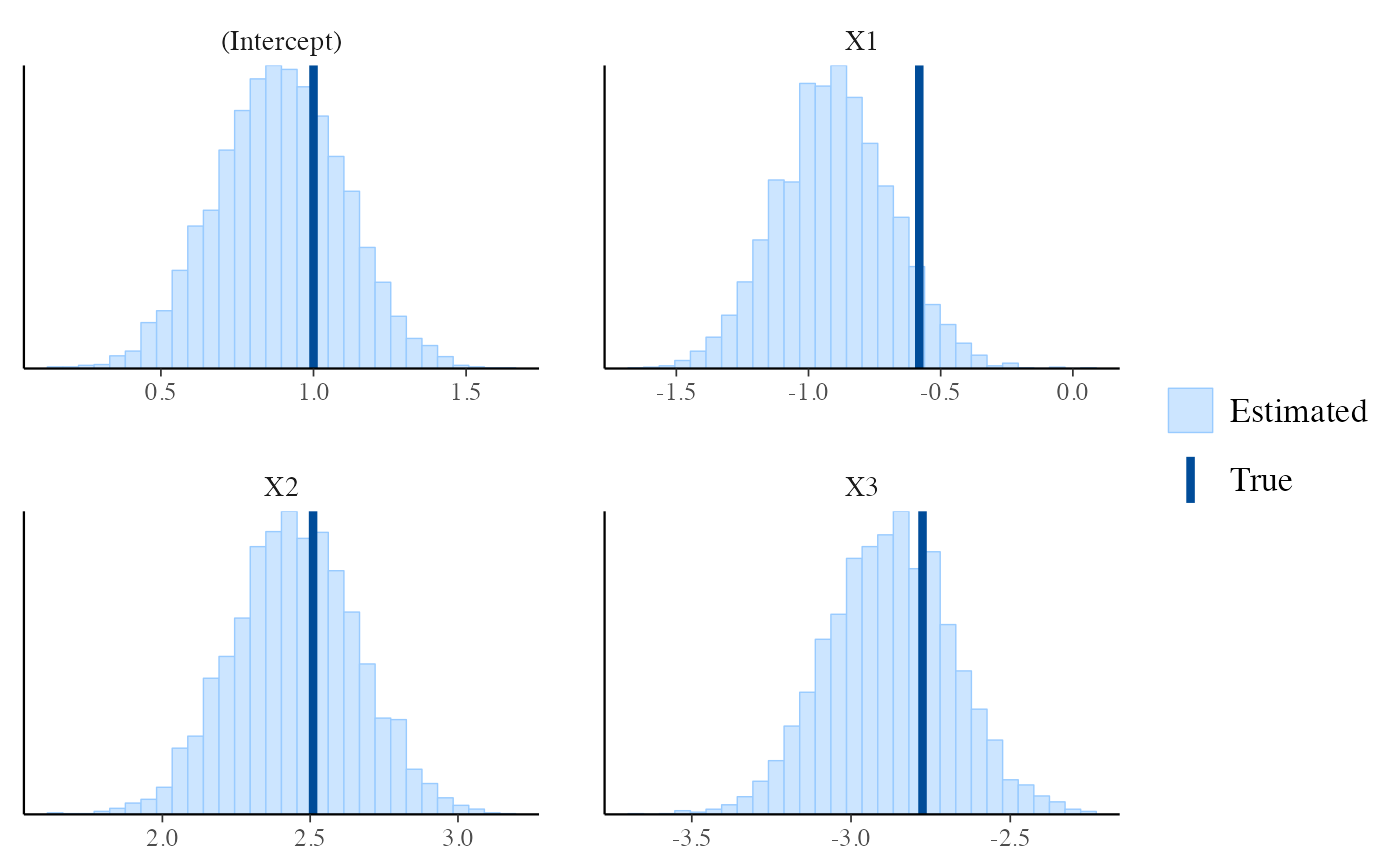
mcmc_recover_hist(): Histograms of the draws for each parameter with the "true" value overlaid as a vertical line.

Examples

# \dontrun{
library(rstanarm)
alpha <- 1; beta <- rnorm(10, 0, 3); sigma <- 2
X <- matrix(rnorm(1000), 100, 10)
y <- rnorm(100, mean = c(alpha + X %*% beta), sd = sigma)
fit <- stan_glm(y ~ ., data = data.frame(y, X), refresh = 0)
draws <- as.matrix(fit)
print(colnames(draws))
#>  [1] "(Intercept)" "X1"          "X2"          "X3"          "X4"         
#>  [6] "X5"          "X6"          "X7"          "X8"          "X9"         
#> [11] "X10"         "sigma"      
true <- c(alpha, beta, sigma)

mcmc_recover_intervals(draws, true)


# put the coefficients on X into the same batch
mcmc_recover_intervals(draws, true, batch = c(1, rep(2, 10), 1))

# equivalent
mcmc_recover_intervals(draws, true, batch = grepl("X", colnames(draws)))

# same but facets stacked vertically
mcmc_recover_intervals(draws, true,
                       batch = grepl("X", colnames(draws)),
                       facet_args = list(ncol = 1),
                       size = 3)


# each parameter in its own facet
mcmc_recover_intervals(draws, true, batch = 1:ncol(draws))

# same but in a different order
mcmc_recover_intervals(draws, true, batch = c(1, 3, 4, 2, 5:12))

# present as bias by centering with true values
mcmc_recover_intervals(sweep(draws, 2, true), rep(0, ncol(draws))) + hline_0()



# scatterplot of posterior means vs true values
mcmc_recover_scatter(draws, true, point_est = "mean")



# histograms of parameter draws with true value added as vertical line
color_scheme_set("brightblue")
mcmc_recover_hist(draws[, 1:4], true[1:4])
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

# }

Compare MCMC estimates to "true" parameter values

Arguments

Value

Plot Descriptions

See also

Examples